Линейные ДУ первого порядка.

Если обыкновенное дифференциальное уравнение можно привести к виду

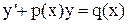, (5)

где p(x) и q(x) функции, не зависящие от y, а только от переменной x, то такое уравнение называется линейным (относительно y).

Линейные ОДУ первого порядка можно решать с помощью подстановки Бернулли 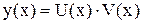, (6)

где U(x) и V(x) две пока неизвестные функции.

Найдем теперь производную по правилу дифференцирования произведения:

(7)

Подставив выражения (6) и (7) для y и y' в уравнение, получим:

Одной из функций U или V можно распорядиться по своему усмотрению. Например, так, чтобы максимально упростить полученное уравнение. Чтобы понять, как наиболее удобно это сделать, вынесем из второго и третьего слагаемых общий множитель U за скобку:

Теперь видно, что если положить , то оставшееся уравнение приобретет простой вид. Таким образом, исходное уравнение распадается на два уравнения, каждое из которых является уравнением с разделяющимися переменными:

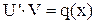
Теперь, найдя из первого уравнения какую-либо функцию V(x), подставим ее во второе и найдем общее решение второго уравнения - функции U(x). А так как решение y(x)=UV, то, значит, мы нашли и его.

Пример. Найти общее решение линейного ДУ: .

Решение.

Поделим уравнение на и перенесем слагаемое в правую часть:

Следуя процедуре, изложенной выше, применим подстановку :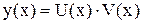

Уравнение распадается на два уравнения с разделяющимися переменными:

Интегрируем . Находим какую-либо функциюV (все V здесь не нужны): . Отсюда Подставляем во второе уравнение

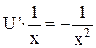
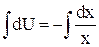
, где С – произвольная постоянная.

Окончательно получаем .

Дата добавления: 2015-07-25