Читайте также:
|
Уравнение Бернулли имеет вид:
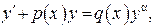(8)
где 
При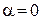 
получаем уравнение с разделяющимися переменными, а при 
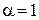- линейное ДУ.
Метод решения уравнения Бернулли тот же, что и для линейных уравнений.
Пример Найти общее решение ДУ:
Решение. Разделим уравнение на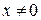 
(х = 0 не является решением данного ДУ):
Полученное уравнение имеет вид (9), следовательно, это уравнение Бернулли. Сделаем замену 
Получим:
| 
|
Таким образом, общее решение ДУ:
Отметим, уравнение имеет решение y = 0 (это проверяется непосредственно). А так как оно не может быть получено из общего решения ни при каком значении константы С, то является особым решением.
Дата добавления: 2015-07-25; просмотров: 39 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Линейные ДУ первого порядка. | | | ДУ, допускающие понижение порядка. |