Читайте также:
|
Пусть система автоматического регулирования описывается линейным дифференциальным уравнением с правой частью
(7.4)
Для отыскания полного решения этого дифференциального уравнения необходимо найти частное или вынужденное решение уравнения с правой частью 
и определить корни характеристического уравнения
Как указывалось выше, полное решение будет иметь вид
(7.5)
Дальнейшим шагом является отыскание произвольных постоянных интегрирования С1,..., Сп. Для этой цели используются начальные условия: при t=0 х(0) = х0, х' (0) = х'0,..., х(n-1)(0) = х0(n-1). Начальные условия накладываются на основании физических соображений или находятся из дифференциального уравнения (7.4). Дифференцируя уравнение (7.5) по времени n-1 раз и используя начальные условия, получают n алгебраических уравнений, куда входят n неизвестных постоянных интегрирования. Совместное решение этих уравнений дает возможность определить искомые постоянные интегрирования С1,..., Сп.
Операции вычисления корней и совместного решения алгебраических уравнений являются трудоемкими. Это особенно относится ко второй операции, так как вычисление корней может быть сделано довольно быстро приближенными методами. В связи с этим использование этого метода построения кривой переходного процесса ограничивается случаем сравнительно невысокого порядка дифференциального уравнения, обычно не выше третьего.
Расчеты получаются более простыми в том случае, когда правая часть (7.4) равна нулю, т. е. имеется однородное дифференциальное уравнение. Тогда частное решение равно нулю и полное решение (7.5) приобретает более простой вид:
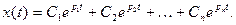(7.6)
В этом случае переходный процесс определяется только видом корней и начальными условиями. В табл. 7.1 для этого случая приведены формулы
Таблица 7.1
| n | Вещественные корни | Комплексные корни |
| — | |
| 
| |
| 
|
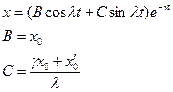
для получающегося переходного процесса при различных степенях дифференциального уравнения n (от 1 до 3) и корнях различного вида. В таблице приняты следующие обозначения:
— абсолютные значения вещественных некратных корней; 
и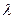 
—абсолютные значения вещественной и мнимой частей комплексного корня; 
— начальное значение исследуемой координаты;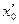 
— начальное значение скорости изменения исследуемой координаты; 
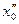— начальное значение ускорения.
Дата добавления: 2015-07-25; просмотров: 52 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Общие соображения | | | Использование преобразований Фурье, Лапласа и Карсона — Хевисайда |