Статические и астатические системы

Кроме задающего воздействия, к разным точкам автоматической системы обычно приложены возмущающие воздействия, от характера и точек приложения которых зависят ошибки системы. Одна и та же система может быть по отношению к одним воздействиям статической, а по отношению к другим — астатической.

Сначала дадим определение статизма и астатизма системы по отношению к адающему воздействию. Для оценки точности АС в установившихся процессах обычно выбирают три типа воздействий: Х_вк = const; Х_вх (t)=vt; Х_вх (t)= .

Система называется статической, если при любом постоянном задающем воздействии Х_вк = const установившаяся ошибка не равна нулю.

Система называется астатической, если при любом постоянном задающем воздействии установившаяся ошибка равна нулю.

Астатические системы могут быть первого, второго и более высоких порядковастатизма.

Астатические системы первого порядка не имеют ошибки по положению (при Х_вк = const), однако имеют постоянную ошибку по скорости (при Х_вх (t)=vt) и возрастающую ошибку по ускорению.

Астатические системы второго порядка не имеют ошибок по положению и по скорости, однако имеют постоянную ошибку по ускорению (при Х_вх (t)= )

Теперь рассмотрим структурные признаки статизма и астатизма автомати­ческих систем. Передаточную функцию разомкнутой минимально-фазовой си­стемы во всех случаях можно представить в виде

(94)

где k — общий коэффициент передачи разомкнутой системы; v — количество интегрирующих звеньев (порядок астатизма); W* (р) — передаточная функция, не содержащая интегрирующих и дифференцирующих звеньев.

Число интегрирующих звеньев в выражении (94) определяет порядок аста­тизма АС.

Статическая система имеет нулевой порядок астатизма (v = 0). Это зна­чит, что в ее прямой цепи нет интегрирующих звеньев. Она может содержать только статические звенья: усилительные, апериодические, запаздывающие, форсирующие и колебательные. Следовательно, такая система даже при Х_вк = const принципиально не может работать без установившейся ошибки (при и 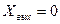). При сложном задающем воздействии Х_вх (t)= статическая система имеет в установившемся режиме не только ошибку по положению, но и ошибки по скорости и ускорению.

Астатическая система первого порядка (v = 1) имеет один интегратор в прямой цепи. При Х_вх = const после завершения переходного процесса ошибка , а равенство X _вых = Х_вх обеспечивается благодаря свойствам интегра­тора как запоминающего устройства (память идеального интегратора беско­нечна). При Х_вх =Vt постоянная скорость изменения выходной величины системы обеспечивается интегратором при const. Это рассогласование называется ошибкой по скорости.

Введение в автоматическую систему двух интегрирующих звеньев (v = 2) позволяет получить управление по ускорению. Система с астатизмом второго порядка благодаря свойствам интеграторов точно воспроизводит в установив­шемся процессе постоянные и линейно возрастающие воздействия. Воздейст­вие, изменяющееся с постоянным ускорением а, система воспроизводит (копи­рует) с постоянной динамической ошибкой, называемой ошибкой по ускорению.

В зависимости от порядка астатизма общий коэффициент передачи разомк­нутой системы k, как видно из рис. 86 и формулы (94), имеет свои индексы

  Рис. 86. Структурная схема астатической системы (v>1)

Рис. 87. Структурные схемы системы для определения порядка астатизма v по возмущению (а) и по задающему воздействию(б)

и называется по-разному: k_s — коэффи­циент передачи статической системы; k₀.— коэффициент передачи астатиче­ской системы первого порядка, или добротность системы по скорости, сек ^-1; k_a — коэффициент передачи аста­тической системы второго порядка, или добротность системы по ускорению, сек ^-2

Таким образом, порядок астатизма по отношению к задающему воздействию легко определить непосредственно по структурной схеме системы. Для этого систему следует привести к одно­контурной и определить количество интегрирующих звеньев между ее вхо­дом и выходом.

Определим теперь порядок астатиз­ма системы (рис. 85) по отношению к возмущающему воздействию F (t). Для этого преобразуем данную систему та­ким образом, чтобы ее часть с переда­точной функцией W ₁(p) по отношению к возмущению F (р) являлась цепью обратной связи (рис. 87, а):

где к_о.с — коэффициент обратной связи; v — количество интегрирующих звеньев; W*₁ (р) — передаточная функция, содержащая только статические звенья.

Очевидно, что при F (t) = const ошибка влияния возмущения может быть равной нулю после завершения переходного процесса только при наличии интегратора в цепи обратной связи v 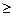1.

Таким образом, если в цепи обратной связи между выходом системы и точ­кой приложения

возмущающего воздействия имеется интегрирующее звено, то система по отношению к этому воздействию является астатической, причем порядок астатизма зависит от количества интегрирующих звеньев v. При от­сутствии интеграторов в цепи обратной связи v = 0 система статическая.

Сформулированное выше правило можно обобщить и на случай определения порядка астатизма по отношению к задающему воздействию. Для этого необ­ходимо структурную схему (рис. 86) преобразовать к виду, показанному на

88. Структурная схема следящей системы с задающим и возмущающим воздействиями.

рис. 87, б, где выходом системы считается ошибка ∆ Х (р). Заметим, что при этом в цепи обратной связи окажется передаточная функция разомкнутой системы.

Пример 5. Определим передаточные функции следящей системы, изображенной на рис. 88, и порядок ее астатизма по отношению к воздействиям Х_вх(p) и F (р).

Непосредственно из структурной схемы видно, что по отношению к задающему воздействию система имеет астатизм первого порядка (v = 1), так как в ее прямой цепи есть одно интегрирующее звено. Передаточная функция разомкнутой системы

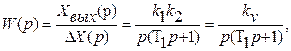
где k_v =k₁ k₂

Основная передаточная функция замкнутой системы

где - постоянная времени; — относительный коэф­фициент затухания.

При 0 < < 1 замкнутая система по своим динамическим свойствам экви­валентна колебательному звену, а при | >= 1 — двум апериодическим звеньям, включенным последовательно.

Передаточная функция ошибки

Сравнение рис. 88 и 87, а показывает, что по отношению к возмущающему воздействию F (р) система является статической, так как ее первое звено апери­одическое и ей присуща ошибка влияния возмущения. Для расчета этой ошибки определяют передаточную функцию по возмущению

Методы исследования динамики и расчета точности автоматических систем на основе результатов структурного анализа будут изложены в последующих бе­седах.

Дата добавления: 2015-07-25