
|
Читайте также: |
Дифференциальное уравнение обыкновенной линейной системы автоматического регулирования, записанное для ошибки регулирования, согласно (5.2) имеет вид
 , (7.1)
, (7.1)
где  — алгебраизированный оператор дифференцирования, g(t) —
— алгебраизированный оператор дифференцирования, g(t) —
задающее воздействие и f(t) — возмущающее воздействие.
Решение линейного дифференциального уравнения с постоянными коэффициентами (7.1) будет

 (7.2)
(7.2)
где  — общее решение однородного уравнения
— общее решение однородного уравнения  , имеющее вид
, имеющее вид
 (7.3)
(7.3)
причем С1,..., Сп — произвольные постоянные, определяемые из начальных условий процесса, а р1,..., рп — корни характеристического уравнения D (р) = 0. Выражение (7.3) записано для случая отсутствия нулевых и кратных корней.
Частное, или вынужденное решение  определяется правой частью-уравнения (7.1), и оно соответствует некоторому установившемуся режиму в системе, который будет существовать после затухания
определяется правой частью-уравнения (7.1), и оно соответствует некоторому установившемуся режиму в системе, который будет существовать после затухания  .
.
Полным решением (7.2) описывается процесс регулирования в линейной системе (общий случай возмущенного движения системы). Первая часть этого-решения  в виде (7.3) представляет собой собственное движение системы, наложенное на частное решение
в виде (7.3) представляет собой собственное движение системы, наложенное на частное решение  .
.
Исходное дифференциальное уравнение системы может быть записано, также для регулируемой величины 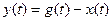 . В системах стабилизации
. В системах стабилизации 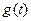 = 0 и поэтому
= 0 и поэтому  .
.
Необходимо обратить внимание на следующее важное обстоятельство. Частное решение  складывается из отдельных слагаемых, отвечающих отдельным членам правой части дифференциального уравнения (7.1). Если действует несколько возмущающих воздействий, то в решении будет соответственно и несколько слагаемых. При этом каждое слагаемое частного решения
складывается из отдельных слагаемых, отвечающих отдельным членам правой части дифференциального уравнения (7.1). Если действует несколько возмущающих воздействий, то в решении будет соответственно и несколько слагаемых. При этом каждое слагаемое частного решения  может определяться по отдельности для каждого возмущающего или задающего воздействия независимо от других, а затем их можно складывать. В этом состоит так называемый принцип суперпозиции.
может определяться по отдельности для каждого возмущающего или задающего воздействия независимо от других, а затем их можно складывать. В этом состоит так называемый принцип суперпозиции.
Следовательно, если имеется дифференциальное уравнение

то частное решение определяющее установившийся процесс в системе, будет иметь три слагаемых, каждое из которых определяется частным решением одного из уравнений:



Несколько иначе обстоит дело с определением переходной составляющей. В решении для переходной составляющей (7.3) произвольные постоянные С1,..., Сп должны вычисляться по начальным условиям обязательно с использова-нием полного выражения решения (7.2), т. е. при исследовании переходных процессов в системах автоматического регулирования всегда надо оговаривать соответствующие внешние условия — задавать g(t) и f(t).
Если переходный процесс ищется как решение однородного уравнения  при заданных начальных условиях системы, то результат такого решения отвечает случаю отсутствия задающих и возмущающих воздействий, причем система совершает свободное движение с какого-то смещенного начального положения. Если же переходный процесс происходит в результате изменения внешних условий (возмущающих сил, изменения нагрузки, перенастройки, изменения режима слежения и т. п.), то этот переходный процесс надо исследовать иначе, с определением произвольных постоянных из полного решения, включающего в себя установившуюся составляющую. Вид воздействия g(t) или f(t) и стоящих перед ними операторных многочленов оказывает существенное влияние на вид переходного процесса.
при заданных начальных условиях системы, то результат такого решения отвечает случаю отсутствия задающих и возмущающих воздействий, причем система совершает свободное движение с какого-то смещенного начального положения. Если же переходный процесс происходит в результате изменения внешних условий (возмущающих сил, изменения нагрузки, перенастройки, изменения режима слежения и т. п.), то этот переходный процесс надо исследовать иначе, с определением произвольных постоянных из полного решения, включающего в себя установившуюся составляющую. Вид воздействия g(t) или f(t) и стоящих перед ними операторных многочленов оказывает существенное влияние на вид переходного процесса.
 При нахождении кривой переходного процесса в системе автоматического регулирования возникают две трудности. Первая трудность — принципиального характера — заключается в том, что в реальных системах регулирования управляющие и возмущающие воздействия не являются известными функциями времени,а носят случайный характер. В связи с этим приходится рассматривать некоторые типовые входные воздействия. Типовые входные воздействия стремятся выбирать так, чтобы они были _ по возможности близкими к реальным воздействиям в системе автоматического регулирования.
При нахождении кривой переходного процесса в системе автоматического регулирования возникают две трудности. Первая трудность — принципиального характера — заключается в том, что в реальных системах регулирования управляющие и возмущающие воздействия не являются известными функциями времени,а носят случайный характер. В связи с этим приходится рассматривать некоторые типовые входные воздействия. Типовые входные воздействия стремятся выбирать так, чтобы они были _ по возможности близкими к реальным воздействиям в системе автоматического регулирования.
|
 и систем стабилизации переходный процесс может строиться для случая приложения возмущающего воздейсвия. В качестве типовых используются возмущающие воздействия в виде единичной ступенчатой функции
и систем стабилизации переходный процесс может строиться для случая приложения возмущающего воздейсвия. В качестве типовых используются возмущающие воздействия в виде единичной ступенчатой функции  и в виде единичной импульсной функции
и в виде единичной импульсной функции  Эти типовые возмущения изображены на рис. 7.1.
Эти типовые возмущения изображены на рис. 7.1.
Входная функция первого типа часто встречается в системах автоматического регулирования и представляет собой внезапный скачок возмущающего воздействия на некоторую постоянную величину, например увеличение тока нагрузки генератора, увеличение момента нагрузки двигателя и т. п. Реакция системы на такое воздействие, построенная для регулируемой величины или для ошибки, отличающихся только знаками  представляет собой переходную функцию системы для данного возмущения.
представляет собой переходную функцию системы для данного возмущения.
 Входная функция второго типа также встречается в системах автоматического регулирования в виде кратковременного удара нагрузки, например при коротком замыкании электрического генератора, которое прекращается через небольшой промежуток времени системой защиты (плавкие предохранители, максималь-ные автоматы и т. п.), при кратковременном возрастании момента нагрузки двигателя и т. д. Реакция сис-темы на воздействие этого типа представляет ее функцию веса. В следящих системах для построения переходного процесса могут приниматься типовые задающие воздействия (рис. 7.2) в виде единичной ступенчатой функции
Входная функция второго типа также встречается в системах автоматического регулирования в виде кратковременного удара нагрузки, например при коротком замыкании электрического генератора, которое прекращается через небольшой промежуток времени системой защиты (плавкие предохранители, максималь-ные автоматы и т. п.), при кратковременном возрастании момента нагрузки двигателя и т. д. Реакция сис-темы на воздействие этого типа представляет ее функцию веса. В следящих системах для построения переходного процесса могут приниматься типовые задающие воздействия (рис. 7.2) в виде единичной ступенчатой функции  или в виде воздействия, изменяющегося по линейному закону
или в виде воздействия, изменяющегося по линейному закону 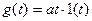 . Воздействие первого типа соответствует, например, в следящих системах воспроизведения угла быстрому повороту командной оси на некоторый угол. Реакция системы
. Воздействие первого типа соответствует, например, в следящих системах воспроизведения угла быстрому повороту командной оси на некоторый угол. Реакция системы 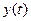 на такое задающее воздействие представляет собой ее переходную функцию для задающего воздействия.
на такое задающее воздействие представляет собой ее переходную функцию для задающего воздействия.
Воздействие второго типа является характерным для следящих систем воспроизведения угла, когда командная ось внезапно начинает двигаться с постоянной скоростью.
Возможно изучение поведения системы регулирования и в том случае, когда входное воздействие представляет собой не детерминированную (определенную), а случайную функцию времени. Этот вопрос будет рассмотрен в главе 11.
Вторая трудность — непринципиального характера — заключается в том, что обычно системы регулирования описываются дифференциальными уравнениями сравнительно высокого порядка. Это усложняет практические расчеты; потому для облегчения задачи построения кривой переходного процесса во многих случаях приходится пользоваться приближенными методами, а также применять вычислительные устройства непрерывного и дискретного действия.
Для построения кривой переходного процесса часто используют численные и графические методы решения дифференциальных уравнений. Таких методов существует много. Применительно к задачам теории автоматического регулирования наиболее удобным оказывается численно-графический метод, разработанный Д. А. Башкировым [98, 121]. Важным достоинством этого метода является то, что он без заметных усложнений может применяться к уравнениям с переменными во времени параметрами и к нелинейным уравнениям. Кроме того, метод Башкирова позволяет с одинаковой простотой строить процессы регулирования при любых заданных внешних воздействиях, в том числе и заданных графически или в виде таблиц. Для получения переходных процессов с большим успехом и весьма широко применяются также вычислительные машины. Различаются вычислительные машины непрерывного и дискретного (цифровые) действия. Они строятся на электронных, полупроводниковых и электромеханических элементах.
Для сложных автоматических систем в настоящее время этому методу отдается предпочтение. Важно отметить, что при использовании вычислительных машин часто можно обходиться без составления дифференциальных уравнений тех звеньев автоматической системы, для которых имеются действующие макеты. Тогда для остальной части звеньев набираются их дифференциальные уравнения на вычислительной машине, к которой подключаются имеющиеся действующие макеты. Это свойство можно использовать для испытания и настройки регуляторов в лабораторных условиях.
Ниже будет рассмотрена часть наиболее распространенных методов построения кривой переходного процесса. К ним относятся метод непосредственного решения линейных дифференциальных уравнений или так называемый классический метод, использование преобразований Фурье, Лапласа и Карсона — Хевисайда, метод трапецеидальных вещественных частотных характеристик и использование вычислительных машин.
В дальнейшем изложении будем рассматривать построение переходного процесса для ошибки 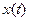 . Однако методика остается единой и для других случаев построения переходного процесса, например для отыскания
. Однако методика остается единой и для других случаев построения переходного процесса, например для отыскания 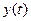 при
при 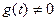 .
.
Дата добавления: 2015-07-25; просмотров: 59 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ | | | Непосредственное решение исходного дифференциального уравнения. |