Читайте также:
|
Для практической оценки погрешности решения дифференциального уравнения проводят вычисления с шагами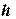 
и 
. За оценку погрешности решения, полученного с шагом , принимают величину, равную
где 
- значение сеточной функции в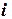 
-й точке, вычисленное с шагом ;
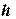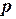- порядок точности, равный 
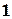для метода Эйлера, 2 для модифицированного метода Эйлера и 4 для методаРунге-Кутта 4-го порядка.
Для достижения заданной точности вычисления повторяют, последовательно уменьшая шаг. Процесс вычислений заканчивается, когда для очередного значения будет выполнено условие 
, где ε ‑ заданная точность.
Дата добавления: 2015-07-25; просмотров: 59 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод Рунге-Кутта. | | | Разностные методы решения краевой задачи для обыкновенного дифференциального уравнения. |