Читайте также:
|
Интервал 
разделим на 
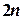отрезков. Группируя узлы тройками 
, на каждом отрезке 
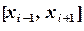
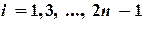интерполируемфункцию 
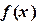полиномом 2-й степени 
По формуле Лагранжа:
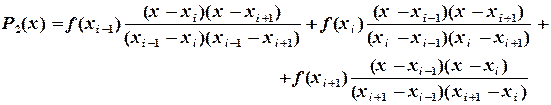
Интегрируя на отрезке 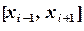, получим:
(5.14)
Суммируяформулу (5.14)по всем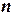 
отрезкам, получаем формулу для приближенного интегрирования (см. рис.5.4):
(5.15)
или
(5.15)
|
| Рис. 5.4. Метод парабол. |
Программа вычисления интеграла методом парабол (Симпсона):
в программе, представленной на рис. 5.2, заменить отмеченные строки на следующие:
1 S=S+(FNF(X)+4*FNF(X+H)+FNF(X+2*H))*H/3
X=X+2*H
Дата добавления: 2015-07-25; просмотров: 58 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод трапеций. | | | Оценка точности вычисления определенного интеграла. |