Приближение функции по методу наименьших квадратов (МНК).

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к лабораторным и самостоятельным работам

по курсам «Информатика» и «Вычислительная математика»

ЧИСЛЕННЫЕ МЕТОДЫ

ЧАСТЬ 2

Казань

УДК 621.313: 518.6

Составители: Ф.Г.Ахмадиев, Ф.Г.Габбасов, Р.Ф.Гиззятов, И.В.Маланичев.

Методические указания к лабораторным и самостоятельным работам

по курсам "Информатика" и «Вычислительная математика». Численные методы. Часть 2. /Казанский государственный архитектурно-строительный университет. Сост.: Ф.Г.Ахмадиев, Ф.Г.Габбасов, Р.Ф.Гиззятов, И.В.Маланичев. – Казань, 2011. – 36 с.

Методические указания состоят из двух частей и предназначены для выполнения лабораторных и самостоятельных работ студентами всех специальностей и направлений подготовки дневного и заочного отделений. В данной части приводятся численные методы аппроксимации функций, вычисления определенных интегралов, решения дифференциальных уравнений и задач линейного программирования.

Рецензент – Р.Б.Салимов, доктор физ.-мат. наук, профессор

Казанский государственный

ã архитектурно-строительный

университет, 2011 г.

Аппроксимация функций.

Приближение функции по методу наименьших квадратов (МНК).

Очень часто в практической работе возникает необходимость найти в явном виде функциональную зависимость между величинам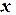и и 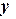, которые получены в результате измерений.

Как правило, общий вид этой функциональной зависимости или так называемой «эмпирической формулы» известен, а некоторые числовые параметры закона неизвестны.

Процесс выражения опытных данных функциональной зависимостью с помощью метода наименьших квадратов состоит из двух этапов: на первом этапе выбирают вид искомой формулы, а на втором этапе для формулы подбирают параметры. Для первого этапа удобно графическое представление зависимости, на втором этапе, в соответствии с идеей МНК, необходимо минимизировать сумму отклонений:

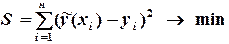(4.1)

где 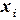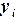_, - значения опытных данных 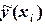- значение функции, вычисленное в точке 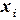; 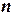- число данных.

Линейная аппроксимация. В случае линейной эмпирической формулы 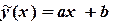и (4.1) принимает вид:

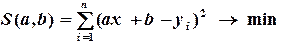(4.2)

Функция (4.2) имеет минимум в точках, в которых частные производные от 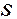по параметрам 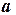и 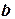обращаются в нуль, т.е.

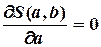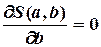, (4.3)

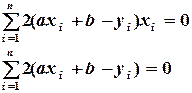
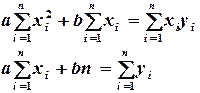(4.4)

Решая систему уравнений (4.4), получим значения 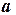и 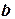уравнения .

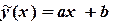Пример 4.1. Подобрать аппроксимирующий полином первой степени 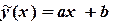для данных

Таблица 4.1.
	0,2	0,9	2,1	3,7

Решение. Для удобства вычисленные значения расположим в таблице.

Таблица 4.2.
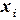
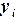
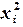
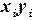
		0,2		0,2
		0,9		0,9
		2,1		4,2
		3,7		14,8
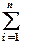
		6,9		20,1

Система для определения коэффициентов имеет вид:

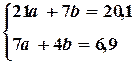(4.5)

Решая систему (4.5), получим следующие значения параметров: 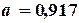, 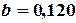. Следовательно, искомый полином имеет вид:

.

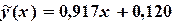Полиномиальная аппроксимация. В случае выбора зависимости в виде полинома, например, 2-й степени 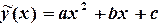и (4.1) принимает вид:

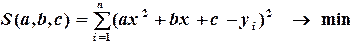(4.6)

Функция (4.6) имеет минимум в точках, в которых частные производные от 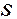по параметрам 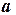, , 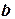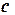обращаются в нуль, т.е.:

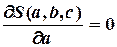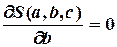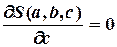, , (4.7)

В результате дифференцирования и элементарных преобразований для определения параметров получают систему из трех линейных уравнений с тремя неизвестными:

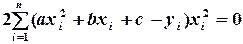
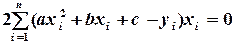
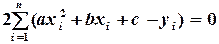
Или

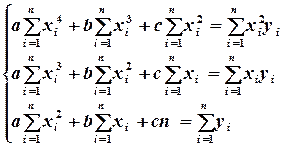(4.8)

Решая систему линейных уравнений (4.8), получим значения 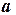, 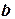и 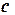уравнения .

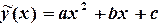Пример 4.2. Используя МНК, построить эмпирическую зависимость 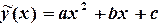, аппроксимирующую следующие табличные значения:

Таблица 4.3.
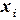
	-2	-1
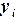
			-1	-2

Решение. Расчеты представим в виде таблицы.

Таблица 4.4.
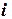
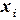
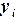
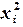
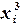
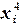
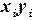
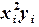
	-2			-8		-12
	-1			-1		-2
		-1
		-2				-2	-2
						-1	-4
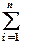
						-18

Тогда система линейных уравнений (4.8) относительно значени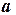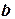й , и 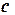примет вид:

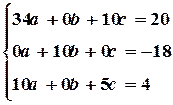(4.9)

Решая систему (4.9), получим следующие значения параметров 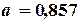; ; 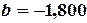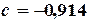. Таким образом, искомый полином имеет вид:

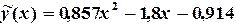
Таблица 4.5.
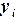
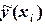
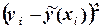
	-2		6,114	0,012
	-1		1,743	0,066
		-1	-0,914	0,007
		-2	-1,857	0,020
		-1	-1,086	0,007

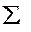
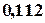
Пример 4.3. Используя программу Excel, построить эмпирическую зависимость вида 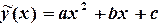, аппроксимирующую значения из таблицы 4.3:

Дата добавления: 2015-07-25