Читайте также:
|
На каждом отрезке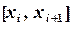 
, 
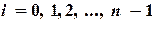функция 
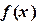заменяется полиномом нулевой степени 
.
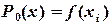Поэтому приближенно I вычисляется по формуле (см. рис. 5.1):
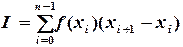(5.3)
|
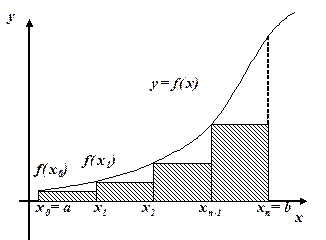
| Рис. 5.1. Метод прямоугольников. |
Для равноотстоящих узлов формула (5.3) имеет следующий вид:
, 
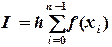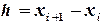(5.4)
Или
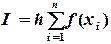(5.5)
Формулу (5.4) называют формулой левых прямоугольников, а (5.5) - правых прямоугольников.
Программа вычисления интеграла методом прямоугольников представлена на рис. 5.2.
| DEF FNF(X)=SQR(2*X^2+1) A=0: B=1 N=8 H=(B-A)/N S=0 X=A 1 S=S+FNF(x)*H X=X+H IF X<B THEN 1 PRINT S END |
| Рис. 5.2. Программа вычисления интеграла методом прямоугольников. |
Дата добавления: 2015-07-25; просмотров: 62 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Численное интегрирование. | | | Метод трапеций. |