Метод Эйлера.

Одним из простейших разностных методов решения обыкновенного дифференциального уравнения является одношаговый метод Эйлера.

Пусть требуется решить задачу Коши для уравнения первого порядка:

(6.5)

на отрезке .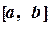

На данном отрезке выбираем некоторую совокупность узловых точек 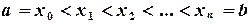и разложим искомую функцию в ряд Тейлора в их окрестностях. Если отбросить все члены, содержащие производные второго и более высоких порядков, и считать узлы равностоящими, т.е. , то это разложение можно записать в виде:

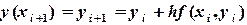, (6.6)

Соотношения (6.6) имеют вид рекурентных формул, с помощью которых значение сеточной функции 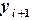в любом узле 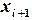вычисляется по ее значению 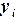в предыдущем узле 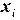. На каждом шаге погрешность имеет порядок 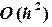. На рис. 6.1 дана геометрическая интерпретация метода Эйлера. В силу невысокой точности формулой Эйлера редко пользуются в практических расчетах и используют более точные методы. Например, модифицированный метод Эйлера.

Рис. 6.1. Метод Эйлера.

Программа решения задачи Коши методом Эйлера дана на рис. 6.2.

CLS DEF FNY(X,Y)=X^2+Y DATA 0, 0.3, 1, 0.1 READ A, B, Y0, H PRINT A;Y0 X=A: Y=Y0 1 Y=Y+ FNY(X,Y)*H X=X+H PRINT X;Y IF X<B THEN 1 END

Рис. 6.2. Программа решения задачи Коши методом Эйлера.

Пример 6.1. Решить задачу Коши методом Эйлера для дифференциального уравнения

на отрезке с шагом

Решение. По формуле (6.6) вычислим значение

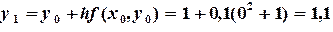
Аналогично вычисляются последующие значения функции в узловых точках

Сеточную функцию записываем в виде таблицы

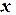
		0,1	0,2	0,3
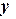
		1,1	1,211	1,3361

Дата добавления: 2015-07-25