Модифицированный метод Эйлера.

Модифицированный метод Эйлера позволяет уменьшить погрешность на каждом шаге до величины вместо 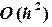в обычном методе (6.6). Запишем разложение функции в ряд Тейлора в виде:

(6.7)

Аппроксимируем вторую производную с помощью отношения конечных разностей:

Подставляя это соотношение в (6.7) и пренебрегая членами порядка , получаем:

(6.8)

Полученная схема является неявной, поскольку искомое значение 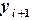входит в обе части соотношения (6.8) и его нельзя выразить явно. Если имеется хорошее начальное приближение , то можно построить решение с использованием двух итераций следующим образом. Сначала по формуле (6.6) вычисляют первое приближение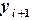

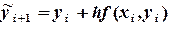(6.9)

Найденное значение подставляется вместо 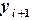в правую часть соотношения (6.8) и находится окончательное значение

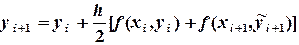(6.10)

На рис. 6.3 дана геометрическая интерпретация первого шага вычислений при решении задачи Коши модифицированным методом Эйлера.

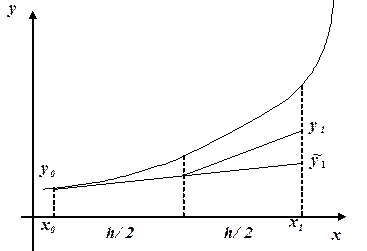
Рис. 6.3. Модифицированный метод Эйлера.

Пример 6.2. Решить задачу Коши модифицированным методом Эйлера для дифференциального уравнения

на отрезке с шагом

Решение. По формуле (6.9) вычислим первое приближение

Используя формулу (6.10), находим окончательное значение в точке

Аналогично вычисляются последующие значения функции в узловых точках

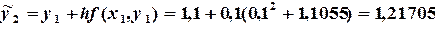
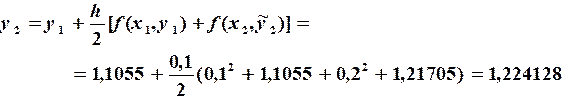
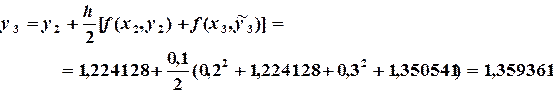
Сеточную функцию записываем в виде таблицы

		0,1	0,2	0,3
		1,1055	1,224128	1,359361

Программа решения задачи Коши модифицированным методом Эйлера отличается от приведенной на рис. 6.2 заменой отмеченных строк на следующие:

1 Y1=Y+ FNY(X,Y)*H

Y=Y+H*(FNY(X,Y)+FNY(X+H,Y1))/2

Пример 6.3. Решить задачу Коши модифицированным методом Эйлера с помощью программы Excel для дифференциального уравнения

на отрезке с шагом .

Дата добавления: 2015-07-25