Порядок решения. 1) Ввести в ячейки A1:D1 заголовки столбцов (рис

1) Ввести в ячейки A1:D1 заголовки столбцов (рис. 6.4).

2) В ячейку A2 – 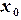0

3) В ячейки B2 и C2 – 1

4) В ячейку D2 – шаг интегрирования 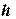0,1

5) В ячейку A3 – значение 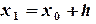=A2+$D$2

6) В ячейку B3 – формулу =C2+$D$2*(A2^2+C2)

7) В ячейку С3 – формулу 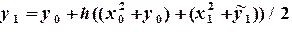=C2+$D$2*(A2^2+C2+A3^2+B3)/2

8) Выделить ячейки A3:С3 и при помощи маркера заполнения ввести формулы в ячейки A4:С4 … A13:С12.

9) Столбцы A и С содержат решение.

		A	B	C	D
		x	y~	y	h
					0,1
		0,1	1,1	1,1055
		0,2	1,21705	1,2241275
		0,3	1,35054	1,3593609
		0,4	1,504297	1,5150438
		0,5	1,682548	1,6954234
		0,6	1,889966	1,9051928
		0,7	2,131712	2,1495381
		0,8	2,413492	2,4341896
		0,9	2,741609	2,7654795
			3,123027	3,1504048
Рис. 6.4. Решение задачи Коши модифицированным методом Эйлера с помощью программы Excel.

Дата добавления: 2015-07-25