Порядок решения. 1) Аппроксимирующая функция должна иметь экстремум в виде пика

1) Аппроксимирующая функция должна иметь экстремум в виде пика. Выберем следующую функцию, зависящую от трех параметров :
;

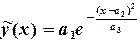2) Ввести в ячейки A2, B2, C2 (рис. 4.4) начальные значения параметров , например 1 1 1

3) В ячейки A5:A11 – значения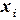

4) В ячейки B5:B11 – значения

5) В ячейку C5 – формулу аппроксимирующей функции (на ячейки с параметрами абсолютные ссылки): =$A$2*EXP(-((A5-$B$2)^2)/$C$2)

6) Скопировать формулу в ячейки C6:C11

7) В ячейку D5 – формулу квадрата разности: =(B5-C5)^2

8) Скопировать формулу в ячейки D6:D11

9) В ячейку D12 – сумму квадратов: =СУММ(D5:D11)

10) Вызвать окно Поиск решения. В настройках указать:

Установить целевую ячейку $D$12

Равной минимальному значению

Изменяя ячейки $A$2:$C$2

11) Нажать кнопку Выполнить.

12) Подтвердить сохранение найденного решения.

13) Рабочий лист изменился и содержит решение (рис. 4.4):

Таким образом, аппроксимирующая данные табл. 4.9 функция имеет вид:

	A	B	C	D	E
	a1	a2	a3
	1,815599	2,450734	0,968182
	x	y	y~	квадрат разности
		0,3	0,206516	0,00873931
	1,5	0,7	0,713777	0,000189808
		1,4	1,471935	0,005174633
	2,5	1,9	1,811053	0,007911556
		1,3	1,329506	0,000870603
	3,5	0,5	0,582326	0,006777524
		0,3	0,15218	0,021850689
			сумма:	0,051514122
Рис. 4.4. Аппроксимация данных нелинейной функцией с тремя параметрами с помощью программы Excel.

Рис. 4.5. Результаты аппроксимации функцией с тремя параметрами.

Точность аппроксимации можно оценить среднеквадратической ошибкой

,

которая не должна превышать погрешность исходных данных.

4.2. Интерполяционный полином в форме Лагранжа.

При решении дифференциальных, интегральных уравнений численными методами вместо искомой функции, обычно, определяют ее значения в отдельных точках (узлах). На следующем этапе проводят восстановление аналитической функции по заданным узлам. Интерполяция интересует нас главным образом как один из способов построения многочлена, приближающего функцию на данном отрезке.

Пусть на некотором промежутке заданы 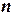различных узлов 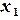, , 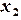, 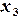…, , 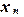а также значения некоторой функции 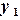, , 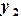, 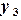…, 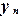в этих узлах. Необходимо построить полином 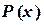, проходящий через заданные точки, т.е.

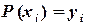
Этот полином называется интерполяционным полиномом, является единственным полиномом степени , и может быть записан, например, в форме Лагранжа или Ньютона.

Интерполяционный полином Лагранжа имеет следующую формулу:

(4.11)

где -фундаментальные полиномы Лагранжа. Они удовлетворяют равенствам

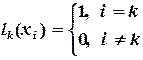(4.12)

и зависят лишь от заданных узлов 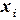, но не от значений интерполируемой функции .

Пример 4.5. Пусть задана таблица:

Таблица 4.10

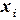
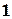
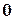
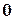
Необходимо построить интерполяционный полином Лагранжа, проходящий через заданные точки

Решение. Запишем фундаментальные полиномы Лагранжа:

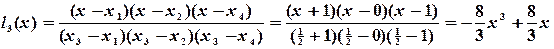
Проверим свойство (4.11), например, для :

, , ,

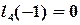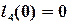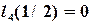Подставляя в полином Лагранжа находим:

Дата добавления: 2015-07-25