Показательно-степенные уравнения и неравенства

Показательно-степенные уравнения и неравенства – это такие уравнения или неравенства, в которых неизвестная входит одновременно и в показатель степени и в основание степени. Например, есть показательно-степенное выражение.

В общем случае показательно-степенное выражение записывается в виде . Допустимые значения переменной, входящей в основание и показатель степени обычно определяются из следующих условий: показатель может принимать любые значения, а основание положительные значения. При этих условиях, сложное показательно-степенное выражение можно представить в виде .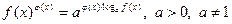

При указанных ограничениях, решением уравнения будет считаться решение смешанной системы и те значения переменной x, при которой , т.е. совокупности системы и уравнения.

Уравнение вида обычно решается логарифмированием левой и правой частей уравнения. Естественно, при этом накладываются ограничения .

Однако выражение может иметь смысл и при некоторых значениях 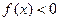. Это приходится иногда учитывать при решении уравнений. Так, например, уравнение 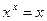кроме корня

x = 1 имеет еще и корень x = -1. В таких случаях для решения уравнений необходимы дополнительные исследования.

При решении показательно-степенных неравенств требуют, чтобы основание степени было положительно. Такие неравенства удобно решать методом интервалов.

Пример 1. Решить уравнение .

Решение. Так как , то исходное уравнение эквивалентно совокупности 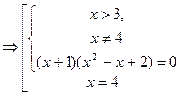. Отсюда имеем . Проверим еще случай, когда основание , т.е. x = 2. Проверкой убеждаемся, что 2 тоже корень: .

Ответ: -1, 2, 4.

Пример 2. Решить неравенство .

Решение. Основание для всех x. Прологарифмируем левую и праую части неравенства по основанию 10. Так как 10 > 1, то знак неравенстве не изменится. Имеем: . Будем решать полученное неравенство методом интервалов. Левая часть неравенства обращается в ноль при , причем, 0 имеет кратность 2.

Ответ: .

Дата добавления: 2015-07-25