Показательные уравнение и неравенства

Показательным называются уравнения, в которых неизвестная входит только в показатель степени. Основание - постоянное

число. Простейшее показательное уравнение 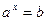или 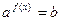. Они решаются сведением правой и левой части к одному основанию или логарифмированием правой и левой части.

Например: .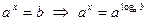

При решении уравнений используются свойства степеней:

1)

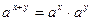
2)

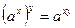
3)

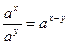
4)

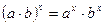
5)

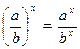
При решении показательных неравенств используются следующие свойства:

Из неравенства 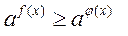следует:

Если a > 1, то 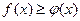, так как функция 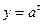возрастает.

Если 0 < a < 1, то 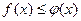, так как функция 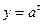убывает.

Аналогичн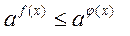о , то

Если a > 1, то 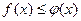, так как функция 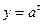возрастает.

Если 0 < a < 1, то 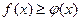, так как функция 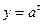убывает.

Методы решения показательных неравенств рассмотрим на примерах.

Пример 1. Решить неравенство .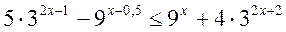

Решение. Преобразуем данное неравенство, приведя его к одинаковым степеням: .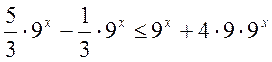

Замена: 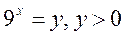. Имеем: 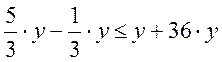или 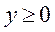. Обратная замена: .

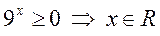Ответ: .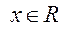

Пример 2. Решить неравенство .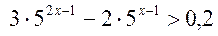

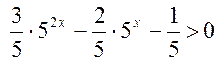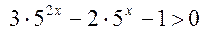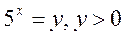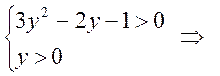
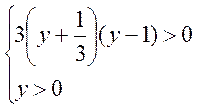
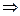
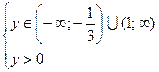
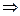
Решение. Имеем: или . Замена: . После замены имеем систему неравенств 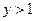или .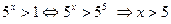

Ответ: .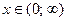

Пример 3. Решить неравенство .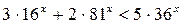

Решение. Такое неравенство называется однородным. Имеем: 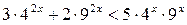. Разделим обе части неравенства на 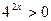. Имеем: 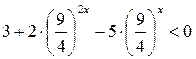. Замена: 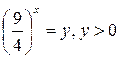. Имеем систему неравенств 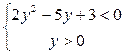. Решение этой системы: 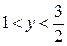Или после обратной замены .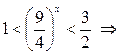

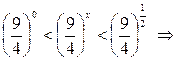
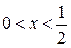Ответ: .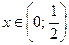

Дата добавления: 2015-07-25