Читайте также:
|
Логарифмические неравенства – это неравенства, содержащие неизвестную под знаком логарифма.
При решении неравенств вида 
необходимо помнить, что логарифмическая функция возрастает при a > 1 и убывает при 0 < a < 1. Поэтому, такое неравенство эквивалентно системе 
при a > 1 и системе 
при 0 < a < 1.
При решении логарифмических неравенств необходимо помнить общие свойства неравенств, свойство монотонности логарифмической функции и область ее определения.
Пример. Решить неравенство 
.
Решение. Так как 
, то 
. Следовательно, 
. Замена: 
. Имеем: 
или 
. Решением этого неравенства будет 
. Обратная замена: 
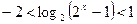, т.е. 
. Отсюда 
или 
.Представив числа 
и 3 в виде степеней с основанием 2, получим: 
. Следовательно, 
.
Ответ: 
.
Дата добавления: 2015-07-25; просмотров: 49 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Логарифмические уравнения | | | Показательно-логарифмические уравнения и неравенства |