Читайте также:
|
Определение. Логарифмом числа b (b > 0) по основанию a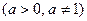 
, называется показатель степени, в которую нужно возвести основание a, чтобы получить число b.
Таким образом, запись 
означает
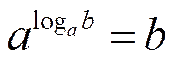
Это основное логарифмическое тождество.
Запись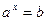 
и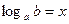 
имеют одинаковый смысл.
Если a = 10 то пишут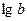 
, если a = e, то 
.
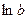Дата добавления: 2015-07-25; просмотров: 41 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Показательные уравнение и неравенства | | | Свойства логарифмов |