Логарифмические уравнения

Логарифмические уравнения – это уравнения, содержащие неизвестную под знаком логарифма.

Простейшие логарифмические уравнения – это уравнения вида , 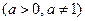. Его решение .

Логарифмические уравнения вида , 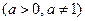эквивалентны одной из следующих систем: 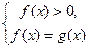или . Решать можно ту из двух систем, которая проще.

Если мы будем решать только уравнение , то могут появиться посторонние корни. Поэтому, в этом случае необходимо сделать проверку, подставив корни в исходное уравнение, либо отбросить те из них, которые не удовлетворяют неравенствам или .

Имеются два основных метода решения логарифмических уравнений: 1) метод, заключающийся в преобразовании исходного уравнения к виду ; 2) метод введения новой переменной.

При решении логарифмических уравнений необходимо помнить свойства логарифмов.

Пример. Решить уравнение .

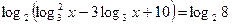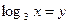Решение. Так как , то . Отсюда . Сделаем замену: . Имеем 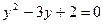. . 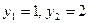Следовательно, или 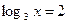. Отсюда .

Ответ: 3; 9.

Дата добавления: 2015-07-25