Читайте также:
|
Пусть X и Y заданные множества. Если определен закон, по которому каждому элементу x Î X соответствует определенный элемент y Î Y, то говорят, что задано отображение X ® Y или функция f: X ® Y (y = f (x)). Функция f: X ® Y называется взаимно однозначной, если каждый элемент y Î Y соответствует только одному элементу x Î X. В этом случае можно определить обратное отображение f -1: Y ® X. Отображение f -1: Y ® X называется обратным к отображению f: X ® Y, если каждому элементу y Î Y ставится в соответствие тот элемент x Î X, для которого y = f (x).
Область определения мы привыкли обозначать D, а область значений E. Пусть f: D(f) ® E(f) - взаимно однозначная функция, т.е. " x Î D (f) $ y Î E (f) и " x 1, x 2 Î D (f), x 1 ≠ x 2 Þ f (x 1) ≠ f (x 2). В этом случае существует обратное отображение f -1: E(f) ® D(f). При этом записи x = f -1(y) и y = f (x) на плоскости определяют одно и то же множество точек. Если у обратного отображения x = f -1(y) аргумент обозначить x, а зависимую переменную y, то получим обратную функцию y = f -1(x), для которой D (f -1) = E (f) и
E (f -1) = D (f).
Если функция f -1 является обратной к функции f, то функция f является обратной к функции f -1. Поэтому функции f и f -1 называются взаимно обратными.
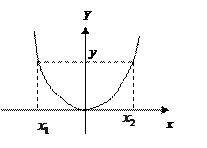Не всякая функция имеет обратную. Например, функция
y = x 4, D (f) = R, E (f) = [0; ¥) не имеет обратной.
Действительно, $ y Î E (f) соответствует два элемента из D (f).
Следовательно, обратное отображение однозначно не определяется.
Функция называется обратимой, если для нее существует обратная функция. Широкий класс обратимых функций образуют монотонные (возрастающие или убывающие) функции. Существуют немонотонные обратимые функции.
Пример. Найти обратную функцию для функции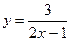 
.
Решение. Область определения 
- это множество 
. Заданная функция не является монотонной на нем. Действительно, 
и, значит, 
(функция не является убывающей). В то же время 
(функция не является возрастающей). Однако можно определить однозначное обратное отображение формулой 
. Поменяв здесь местами x и y получим обратную функцию 
для заданной функции f.
Отметим, что графики взаимно обратных функций 
и 
симметричны друг другу относительно биссектрисы первого и третьего квадрантов.
Для взаимно обратных функций f и 
имеют место равенства:
,
.
Дата добавления: 2015-07-25; просмотров: 40 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Свойства логарифмов | | | Логарифмическая функция |