Читайте также:
|
Показательно-логарифмические уравнения и неравенства – это уравнения и неравенства, содержащие неизвестную в основании и в показателе степени, при этом показатель степени содержит логарифмы.
Например, показательно-логарифмическим уравнением является уравнение типа 
.
Такие уравнения можно решать логарифмированием правой и левой частей уравнения по основанию a.
При решении неравенств нужно помнить о свойствах монотонности логарифмической функции.
Пример 1. Решить уравнение 
.
Решение. Прологарифмируем по основанию 10 правую и левую части. 
. Имеем: 
или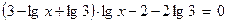 
. Замена: 
. Имеем квадратное уравнение 
. Его корни: 
.
Обратная замена: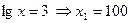 
, 
.
Ответ: 30; 100.
Пример 2. Решить неравенство 
.
Решение. Прологарифмируем обе части неравенства по основанию 10. Так как функция - возрастающая, то знак неравенства не изменится. 
.
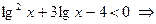
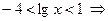
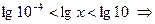
Ответ: 
.
Дата добавления: 2015-07-25; просмотров: 135 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Логарифмические неравенства | | | Показательно-степенные уравнения и неравенства |