
Читайте также:
|
Потенциальная кривая гармонического осциллятора представляет собой симметричную параболу.
Действительные потенциальные кривые двухатомных молекул асимметричны и только в области малых отклонений от равновесия (и малых значений энергии) апроксимируются параболой.
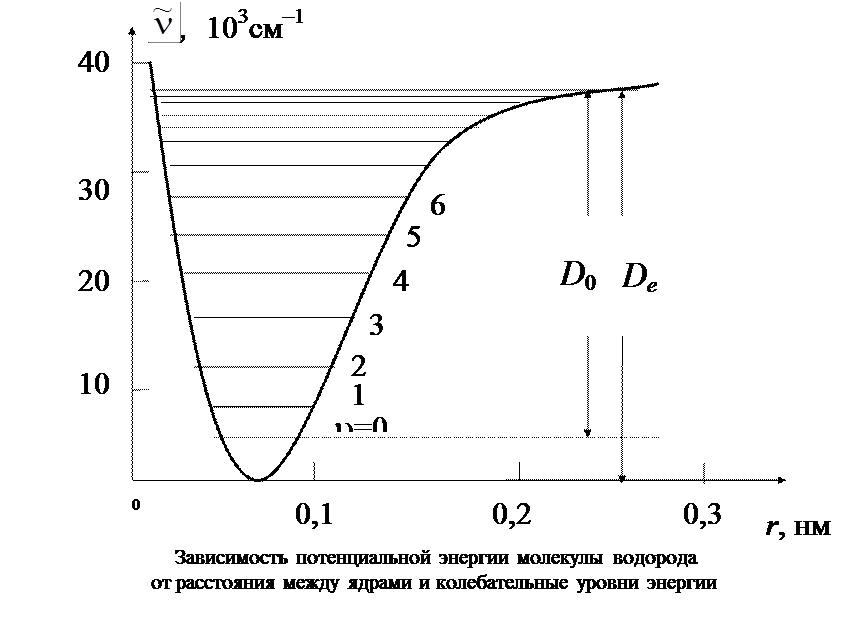
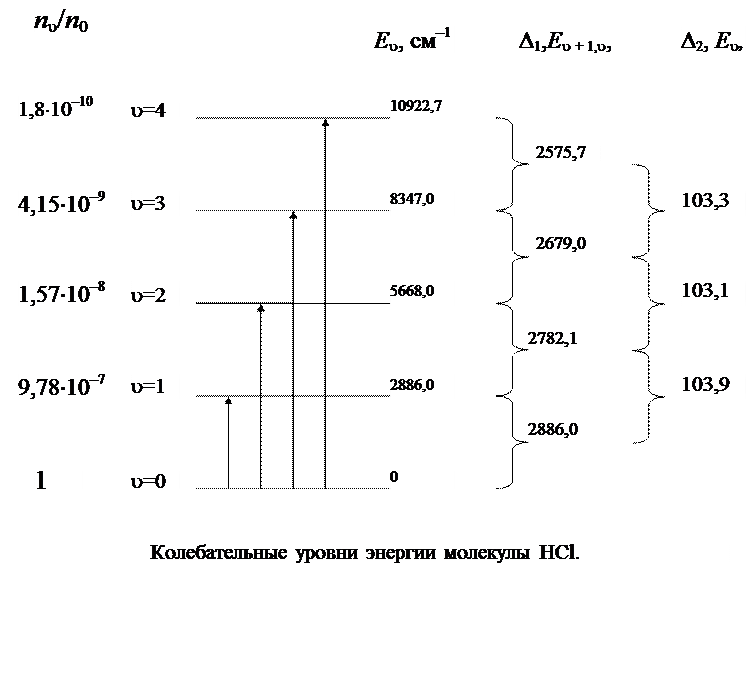
Сближение колебательных уровней с приближением к границе диссоциации связано с тем, что они располагаются тем теснее, чем положе потенциальная кривая.
Приближенная формула, учитывающая ангармоничность, имеет вид
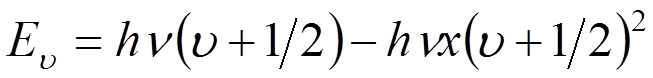 (1)
(1)
(Именно такое выражение получается при задании потенциальной энергии в виде функции Морзе (см. ниже)).
х – константа ангармоничности, по порядку величины равная 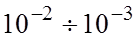 ,
, 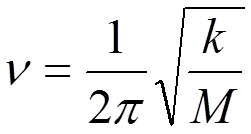
Если энергию, как и волновые числа, измерять в см–1, то формулу (1) можно переписать, опустив постоянную Планка h:
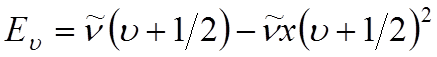 .
.
Нулевая энергия равна 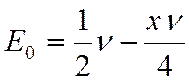 (2)
(2)
Разность энергий между соседними уровнями
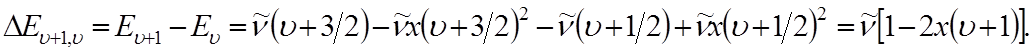 (3)
(3)
 D E u + 1,u,
D E u + 1,u,
0 ® 1 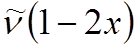 ,
,
1 ® 2 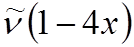 ,
,
2 ® 3 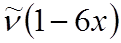 .
.
Вторые разности
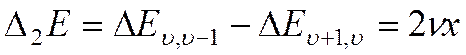 (4)
(4)
не зависят от υ.
Определив из спектра вторые разности и частоту 0-1, найдем ν и x.
Дата добавления: 2015-07-20; просмотров: 219 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Колебательные волновые функции ГО. | | | Энергия диссоциации. |