Читайте также:
|
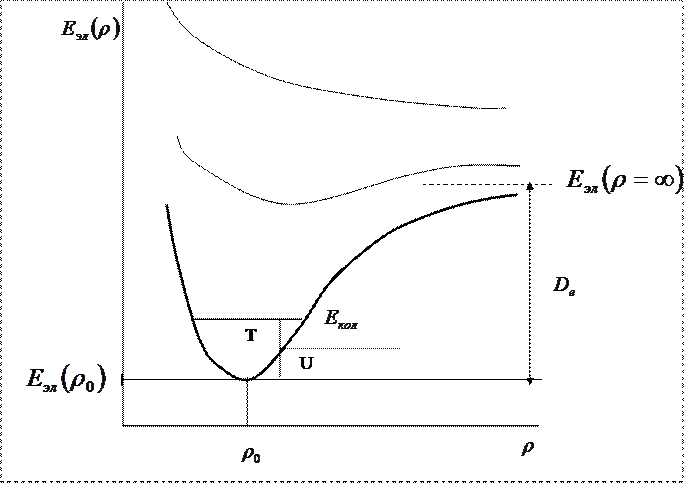
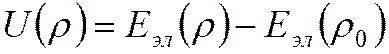
Гармонические колебания двухатомной молекулы (малые колебания)
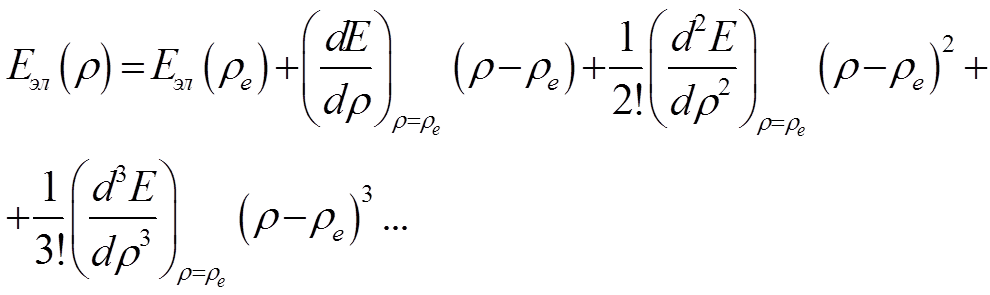
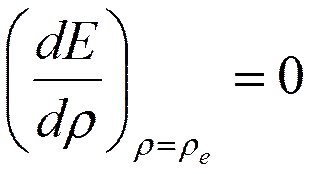-условие минимума
Введем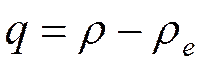 
Обозначим 
Параболический потенциал- задача о колебаниях гармонического осциллятора
Кинетическая энергия 
, где 
- приведенная масса
Решени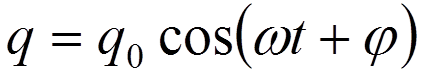е: 
, где
, 
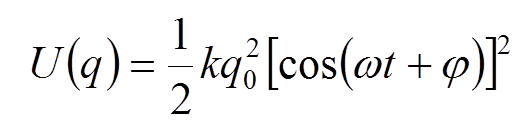
Полная энергия 
.
С учетом 
, перепишем
.
 |
Квантово-механическое решение
, 
, 
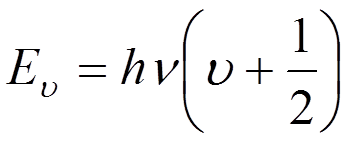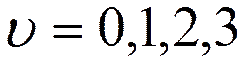
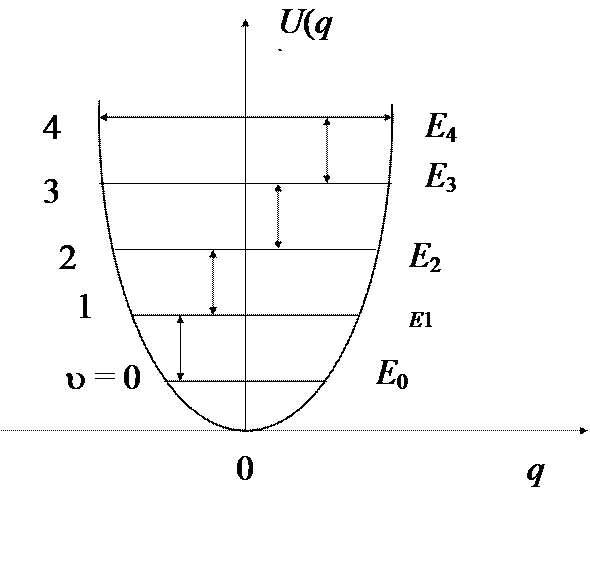
Для гармонического осциллятора в поглощении, испускании и в КР разрешены переходы с 
.
E u+1 – E u = h n,
а частота перехода между этими уровнями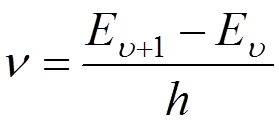 
равна классической частоте.
Энергии квантового осциллятора можно поставить в соответствие амплитуду классических колебаний:
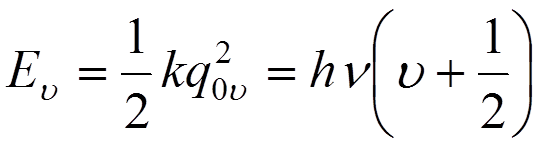
откуда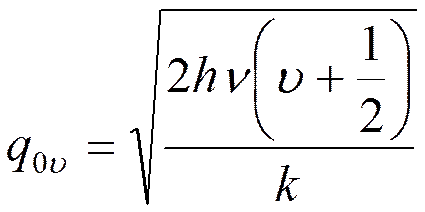 
.
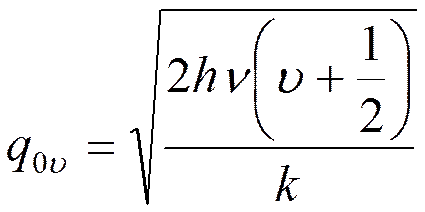Подставив 
, получим
.
Для H2 амплитуда нулевых колебаний 
, что составляет 0,16 от равновесного расстояния 
.
Дата добавления: 2015-07-20; просмотров: 110 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Мы действуем, не оглядываясь на конкурентов | | | Колебательные волновые функции ГО. |