Читайте также:
|
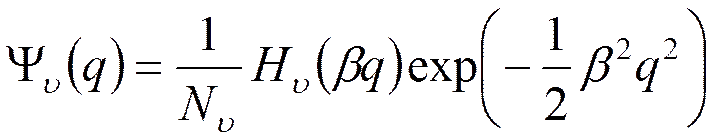
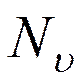- нормировочный множитель, 
,
полиномы Эрмита – полиномы степени 
для 
Обозначим 
Первые четыре полинома Чебышева – Эрмита:
Н 0 (х) = 1, H 1 (х) = 2 х, Н 2(х) = 4 х 2 – 2,
Н 3 (х) = 8 х 3 – 12 х.
(При четном υ – четные функции, при нечетном – нечетные).
Множитель 
в выражении для волновой функции обеспечивает быстрое падение волновых функций за пределами области классического движения.
(слева на рисунке) определяет вероятность различных значений координат. Самые высокие максимумы находятся вблизи поворотных точек классического движения
Дата добавления: 2015-07-20; просмотров: 65 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Зависимость электронной энергии от межъядерного расстояния - потенциальная функция для колебательного движения. | | | Ангармоничность колебаний. Энергия диссоциации. Функция Морза. |