Читайте также:
|
Опираясь на скалярное произведение векторов можно ввести понятие нормы (длины) вектора.
Пусть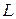 
– унитарное пространство со скалярным произведением 
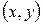. Длиной или нормой вектора 
называется корень квадратный из его скалярного квадрата: 
(имеется ввиду арифметический корень).
При этом 
так же, как и 
, равняется нулю тогда и только тогда, когда 
.
Теорема: Неравенство Шварца: каковы бы ни были векторы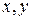 
в унитарном пространстве справедливо неравенство:
. (8.1)
Доказательство:
Если 
, неравенство (8.1) очевидно, т.к. справа стоит неотрицательное число. Поэтому пусть 
. Рассмотрим скалярный квадрат:
.
Это неравенство справедливо при любом 
. Возьмем в качестве 
, где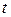 
– любое вещественное число. Тогда имеем:
.
Это неравенство должно выполняться при любом вещественном 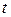. Его левая часть – квадратный трехчлен относительно 
с вещественными коеффициентами. Известно, что он принимает неотрицательные значения (
) тогда и только тогда, когда его дискриминант 
:
. ЧТД.
Можно показать, что равенство здесь будет тогда и только тогда, когда векторы коллинеарны (линейно зависимы).
Частные случаи неравенства Шварца в различных унитарных пространствах.
1) В эвклидовом пространстве (обычном 3-мерном пространстве свободных векторов) со скалярным произведением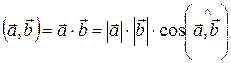 
, где 
неравенство (8.1) очевидно: 
.
2) В 
-мерном арифметическом комплексном пространстве с векторами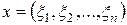 
, 
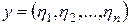, со скалярным произведением и нормой в виде
; 
,
неравенство Шварца (8.1) принимает вид неравенства Коши:
или 
.
3) В пространстве 
всех непрерывных функций на сегменте 
с векторами 
, 
, со скалярным произведением векторов и нормой в виде
; 
неравенство Шварца (8.1) принимает вид неравенства Буняковского:
.
Дата добавления: 2015-07-20; просмотров: 235 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Проверить, что при этом все отмеченные 4 свойства скалярного умножения выполняются. | | | Свойства нормы вектора. |