Читайте также:
|
Унитарное пространство с таким скалярным произведением обозначается 
4) Однако, если в пространстве, например в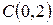 
попробовать ввести скалярное следующим образом: 
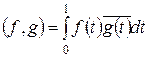, то при этом 4 свойство не будет выполняться: из 
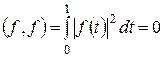с необходимостью не следует, что 
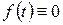на всем сегменте 
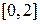: вне сегмента 
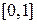она может быть отличной от нуля.
Дата добавления: 2015-07-20; просмотров: 47 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Определение унитарного пространства. Примеры. | | | Норма вектора, неравенства Шварца, Коши, Буняковского. |