Определение унитарного пространства. Примеры.

Лекция 8. УНИТАРНЫЕ ПРОСТРАНСТВА

8.1. Определение унитарного пространства. Примеры.

8.2. Норма вектора, неравенства Шварца, Коши, Буняковского.

8.3. Свойства нормы вектора.

Определение унитарного пространства. Примеры.

Унитарным пространством называется комплексное линейное пространство 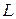, в котором введена операция, сопоставляющая каждой паре векторов 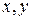число, называемое скалярным произведением – 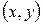, и обладающая следующим свойствами:

1. ;

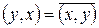2. ;

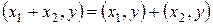3. ;

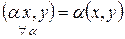4. 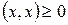, равенство только при .

Унитарное вещественное пространство называется эвклидовым.

Все это – обобщение обычного скалярного произведения в векторной алгебре.

Самостоятельно доказать:

2а. ;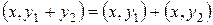

3а.

Из указанных свойств следует, что:

.

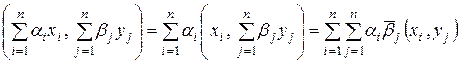Примеры унитарных пространств:

1) Эвклидово пространство – обычное 3-мерное пространство свободных векторов. Скалярное произведение вводится по формуле:

.

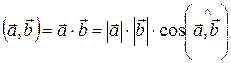2) -мерное арифметическое комплексное пространство с векторам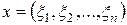и и .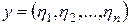

В нем скалярное произведение можно ввести многими способами, например так:

; .

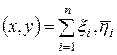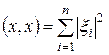Дата добавления: 2015-07-20