Неопределенные степенно-показательные выражения

Рассмотрим теперь степенно-показательное выражение и последовательность при условии, что > 0 " n Î N.

Если для существуют конечные пределы: и , причем a >0, то .

Доказательство опускаем.

Очевидно, что исключительные случаи отвечают таким комбинациям значений a и b:

a = 1, b = ∞; a = 0, b = 0; a = +∞, b = 0.

В этих случаях говорят, что выражение представляет неопределенность вида 1^¥, 0⁰, ∞⁰ (смотря по случаю). Для решения вопроса о пределе последовательности здесь мало знать лишь пределы , а нужно непосредственно учесть закон, по которому они стремятся к своим пределам.

В качестве примера неопределенности вида 1^¥ приведем выражение 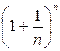. Последовательность , определенная этим выражением, 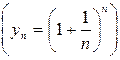имеет конечный предел. По примеру Эйлера, его всегда обозначают буквой е. Это иррациональное число

(1.11)

имеет исключительную важность, как для самого анализа, так и для его приложений. Вот первые семь знаков его разложения в десятичную дробь:

е = 2,718281…

Некоторые свойства числа е делают особенно выгодным выбор этого числа в качестве основания для системы логарифмов. Логарифмы по основанию е называются натуральными и обозначаются знаком ln без указания основания. Десятичные логарифмы связаны с натуральными формулой:

.

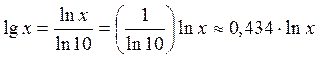Таким образом, поставив себе задачей – определить пределы последовательностей, заданных арифметическими (1.10) или степенно-показательным выражениями, по пределам последовательностей , из которых они составлены, мы нашли случаи, когда этого сделать нельзя: неопределенности вида . В этих случаях приходится, учитывая закон изменения последовательностей , непосредственно исследовать интересующее нас выражение. Подобное исследование получило название раскрытие неопределенности. Общие методы для раскрытия неопределенностей будут даны позже.

Дата добавления: 2015-07-20