Читайте также:
|
Теорема 1. Если последовательность имеет предел, то этот предел единственный.
Доказательство. Допустим противное. Пусть последовательность { yn } имеет два предела lim yn = a и lim yn = b, где a ¹ b, для определенности возьмем a < b.
Выберем e > 0 так, чтобы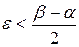 
. Поскольку yn ® a, то найдется такой номер n 1, что для n > n 1 будет выполняться неравенство a - e < yn < a + e. С другой стороны, раз yn ® b, то найдется такой номер n 2,что для n > n 2 окажется b - e < yn < b + e. Если взять номер n большим и n 1, и n 2, то соответствующие значения yn последовательности { yn } будут одновременно принадлежать двум интервалам (a - e, a + e) и (b - e, b + e), которые не пересекаются, т.е. (a - e, a + e) ∩ (b - e, b + e) = Æ, что невозможно. Значит, предположение неверно и для последовательности существует только один предел.
Следствие. Если две последовательности { xn } и { yn } при всех их изменениях равны: xn = yn, причем каждая из них имеет конечный предел: lim xn = a,lim yn = b, то равны и эти пределы: a = b.
Теорема 2. Если последовательность { yn } имеет конечный предел a, то она ограничена, в том смысле, что все ее значения составляют ограниченное множество.
Доказательство. Так как lim yn = a, то в любую e -окрестность точки a попадают все yn, за исключением разве лишь конечного числа точек yn. Пусть начиная с n = ne+ 1 все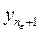 
, 
, 
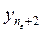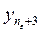,… попали в окрестность (a - e, a + e), т.е. a - e < yn < a + e " n > ne.
Выберем из чисел a - e и a + e наибольшее по модулю m = max (| a - e |,| a + e |). Тогда | yn | < m¢ " n > ne.
Теперь для конечного множества чисел |y 1 |, |y 2 |, |y 3 |, ....,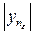 
, m¢ выберем наибольшее m = max(|y 1 |, |y 2 |, |y 3 |, ...., 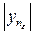, m¢). Тогда " n Î N, следует, что | yn | < m. Теорема доказана.
Заметим, что обратное утверждение не выполняется, так как не всякая ограниченная последовательность имеет предел. Например, последовательность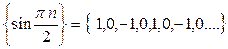 
ограничена, но предела не имеет. Действительно, по определению предела последовательности число a будет ее пределом, если в любой e -окрестности точки a содержится бесконечное множество членов этой последовательности, а вне ее – конечное. В данном случае в любой e -окрестности, например, единицы, e < 1, находится бесконечное множество членов последовательности, но и вне этой окрестности также находится бесконечное множество ее членов. Это означает, что последовательность не имеет предела.
Теорему 2 дополним леммой, доказательство которой аналогично доказательству теоремы 2.
Лемма. Если последовательность { yn }, у которой yn ¹ 0 " n Î N имеет предел, отличный от нуля, то последовательность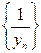 
ограничена.
Справедлива следующая теорема, которую примем без доказательства.
Теорема 3. Если для последовательностей { xn } и { yn }, имеющих конечные пределы a и b, и, начиная с некоторого номера, для всех последующих членов выполняются неравенства xn ³ yn или xn > yn, то lim xn ³lim yn или a ³ b.
Следует обратить внимание на то, что из строгого неравенства xn > yn , вообще говоря, не вытекает строгое же неравенство lim xn > lim yn,а только по-прежнему lim xn ³ lim yn. Так, например,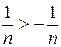 
при всех n, и, тем не менее 
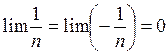. Эта теорема дает возможность осуществлять предельный переход в неравенствах: из xn ³ yn можно заключить, что lim xn ³ lim yn.
Замечание. Знак > всюду может быть заменен знаком <.
Теорема 4.(Гурьева о трех последовательностях). Если для трех последовательностей { xn }, { yn }, { zn }, начиная с некоторого номера, выполняются неравенства xn ≤ yn ≤ zn , причем последовательности { xn } и { zn } стремятся к общему пределу a: lim xn = lim zn = a, то и последовательность { yn } имеет тот же предел: lim yn= a..
Доказательство. Зададимся произвольным e > 0. Поэтому e, прежде всего, найдется такой номер n 1, что при n > n 1 a - e < xn < a + e. Затем найдется такой номер n 2, что при n > n 2 a - e < zn < a + e.
Пусть ne будет больше обоих чисел n 1и n 2; тогда при n > ne выполняются оба предшествующих двойных неравенств и поэтому a - e < xn ≤ yn ≤ zn < a + e.
Окончательно, при n > ne a - e < yn < a + e или | yn - a | < e. Это означает, что lim yn = a.
Дата добавления: 2015-07-20; просмотров: 172 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Определение и геометрическое истолкование предела последовательности | | | Бесконечно малые последовательности и их свойства |