Элементарные функции

К элементарным функциям относятся функции, образованные из основных элементарных функций и чисел посредством четырех арифметических действий и их композиций (сложные функции) последовательно примененных конечное число раз. Например:

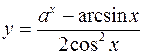и т.п.

Существуют и не элементарные функции. К ним относятся, например, функции y = E (x) – “ целая часть x ” (см. гл.1,§2, п.2.1), функция Дирихле, которая определяется так:

и функция “ сигнум х ”, которая обозначается через signx:

К алгебраическим элементарным функциям относятся:

1. Целая рациональная функция (многочлен)

(1.6)

где и х – действительные числа, n – натуральное число.

Эта функция образована из основной элементарной функции у = x^a,где a Î N, и чисел путем сложения и умножения. Естественная область применения: бесконечный интервал (– ∞, +∞);

2. Дробно – рациональная функция, которая представлена в виде отношения двух целых рациональных функций относительно x

. (1.7)

Областью определения дробно – рациональной функции (речь идет о естественной области применения) является множество всех действительных чисел кроме тех, для которых знаменатель обращается в нуль;

3. Иррациональная функция. Это функция, в которой, кроме указанных выше действий, применяется еще и операция извлечения корня, т.е. в основной элементарной функции y = x^a a может принимать не только целые, но и дробные значения. Область применимости такого выражения устанавливается для каждого конкретного случая отдельно (см., например, гл.1, § 2, п.2.3).

Все прочие элементарные функции (показательные, логарифмические, тригонометрические и др.) относятся к трансцендентным. В качестве примера рассмотрим гиперболические функции. Так называются функции вида

;

;

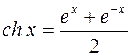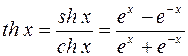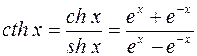
(гиперболический синус, косинус, тангенс, котангенс); они определены для всех значений x,исключая сth x,который теряет смысл при x = 0.

Эти функции проявляют аналогию с тригонометрическими функциями.

Так, имеют место формулы (обратить внимание на знаки):

сh (x ± y) = ch x ch y ± sh x sh y,

sh (x ± y) = sh x ch y ± ch x sh y,

из которых при y = x, в частности, следует:

ch ² x – sh ² x = 1; ch 2 x = ch ² x + sh ² x; sh 2 x = 2 sh x ch x.

Графики гиперболических функций изображены на рис.11.

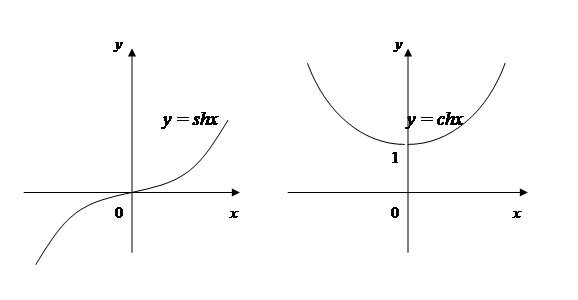
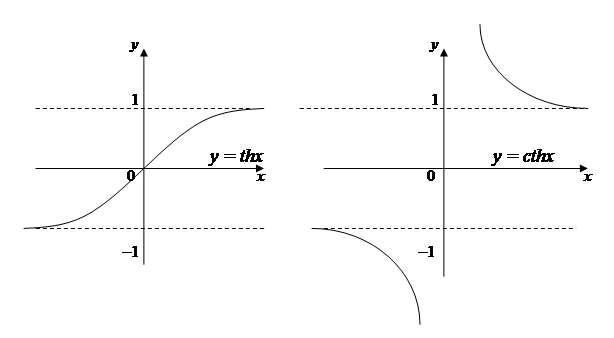
Рис. 11 (Переделать, асимптоты)

Дата добавления: 2015-07-20