
Читайте также:
|
Пусть a и b – действительные числа, причем a < b.
Определение 1. Сегментом или замкнутым промежутком называется множество всех действительных чисел x, удовлетворяющих условию a £ х £ b. Числа a и b называются концами сегмента. Сегмент обычно обозначают [ a, b ].
Геометрическим аналогом сегмента [ a, b ] = { x | a £ x £ b } является отрезок числовой оси, концами которого служат точки a и b. Поэтому вместо слова “сегмент” употребляется также “отрезок”.
Определение 2. Интервалом или открытым промежутком называется множество всех действительных чисел х, удовлетворяющих условию a < х < b. Числа a и b называют концами интервала. Интервал обозначают (a, b) или ] a, b [.
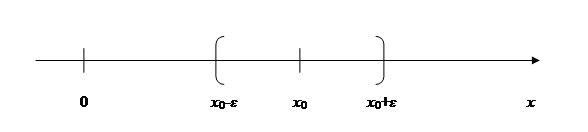
Рис. 1
Рассмотрим интервал (x 0 – e, x 0 + e)с центром в точке x 0 (рис.1). Такой интервал называется e - окрестностью точки x 0 или окрестностью точки x 0 радиусом e.
Определение 3. Полусегментом (полуинтервалом) или полуоткрытым промежутком, замкнутым слева (справа), называется множество всех действительных чисел х,удовлетворяющих условию a £ х < b (a < х £ b).Полуоткрытый промежуток, замкнутый слева, обозначается [ a, b), справа – (a, b ].
Числовые промежутки, рассмотренные выше, представляют собой ограниченное множество P, у которого inf P = a, а sup P = b.
Помимо указанных числовых промежутков приходится рассматривать и бесконечные числовые промежутки, у которых одним из концов или обоими служат " несобственные числа " – ∞ и +∞. Обозначения их аналогичны приведенным выше. Например, (– ∞, +∞) есть множество всех действительных чисел; (a,+∞)означает множество чисел х, удовлетворяющих неравенству х > a;промежуток (– ∞, b ]определяется неравенством х £ b. Геометрически бесконечные промежутки изображаются в виде бесконечной в обе стороны прямой или луча.
Дата добавления: 2015-07-20; просмотров: 244 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Ограниченные числовые множества | | | Графический способ задания функции |