Обратная функция для аналитически заданной функции

Пусть функция у = f (x), заданная аналитическим выражением, определена в некоторой области Р и пусть Е будет множество всех значений, которые эта функция принимает, когда х изменяется в пределах области Р, т.е. Е = f (Р) (обычно как Р,так и Е будут представлять собой числовые промежутки).

Выберем какое-нибудь значение у = у ₀ из области Е; тогда в области Р необходимо найдется такое значение х = х ₀, при котором наша функция принимает именно значение у ₀, так, что f (х ₀) = у ₀, или, разрешив это уравнение относительно х ₀, то

х ₀= g (у ₀). (1.5)

Если каждому значению у из Е ставится в соответствие только одно значение х из Р, то это означает, что аналитическим выражением (1.5) задается функция х = g (у), определенная на Е и со значениями в Р, и во-вторых, что функция у = f (x) представляет собой взаимно однозначное отображение и, следовательно, для нее существует обратная функция f ^{– 1}.

Покажем, что функция g: E ® P является обратной для функции f: P ® E, т.е. g = f ^{– 1}. Действительно, при подстановке x = g (y) в y = f (x) мы получаем тождество y = f [ g (y)] = y,аналогично x = g [ f (x)] = x. Это означает, что композиция (суперпозиция) функций g на f или f на g осуществляют тождественное отображениесоответственно e: y ® y или e: x ® x,т.е. f о g = g о f = e и, следовательно, g = f ^{– 1}.

Теперь рассмотрим ситуацию, когда каждому значению y из E ставится в соответствие не одно, а несколько (например, k) значений x из P, т.е. если y = y ₀, то x = x _{0 i} , i = 1,..., k. Для этого случая функция f: P ® E не представляет собой взаимно однозначное отображение, а аналитическое выражение (1.5) не может определять функцию. Для этой ситуации поступим следующим образом. Разобьем область определения P функции y = f (x) на k подмножеств P _i , i = 1,2, ..., k так, чтобы каждому значению y из E ставилось в соответствие только одно значение x из P _i и при этом f (P _i) = E. Тогда, ограничив область определения функции y = f (x) подмножеством P _i , мы получим ситуацию, аналогичную рассмотренной выше. Откуда следует, что функция y = f (x),на подмножестве P_i , имеет обратную функцию и ею является функция x = g (y), определенная на E, но со значениями в P _i , т.е. f: P _i ® E, а f ^{– 1} = g: E ® P _i.

Если функция x = g (y)является обратной для функции y = f (x), то очевидно графики обеих функций совпадают. Можно, однако, потребовать, чтобы и аргумент обратной функции обозначался буквой x, т.е. вместо функции x = g (y) рассматривать y = g (х).Если при этом по-прежнему значения х откладывать по горизонтальной оси, а значения у – по вертикальной, то графики этих функций будут различны. График обратной функции будет симметричен графику прямой функции y = f (x) относительно биссектрисы первого и третьего координатных углов у = х.

Примеры:

1. y = a^x (a > 0, a ¹ 1) – показательная функция. Эта функция определена на промежутке P = (– ∞, +∞), а значения y заполняют промежуток E = (0,+∞),причем каждому y из этого промежутка отвечает в P одно значение x = log _a y. Таким образом, выражение x = log _a y есть функция, определенная на E и эта функция является обратной для функции y = a^x, определенной на P. Действительно, 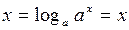, или 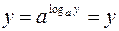. Графики этих функций представлены на рис.2.

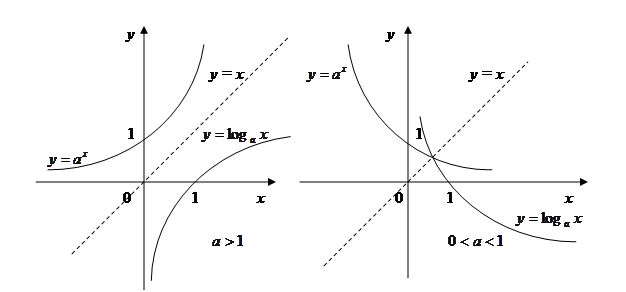
Рис. 2

2. y = xⁿ – степенная функция, где n Î N. Такая функция определена на промежутке R = (-∞, +∞), а значения y заполняют либо промежуток E ₁ = (– ∞,+∞), если n – нечетное число, либо промежуток E ₂ = (0,+∞), если n – четное число.

В первом случае любому y = y ₀ из E ₁ отвечает в P одно значение 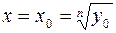или (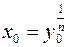) и, следовательно, выражение 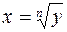определяет обратную функцию для 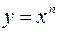. На рис.3 показаны графики прямой (сплошная кривая) и обратной (пунктирная кривая) функций.

Во втором случае функция y = xⁿ, не имеет обратной, так как одному значению у = у ₀ из Е ₂ = (0, +∞) соответствуют два значения x = x _{0 k} , k = 1,2 из P: , .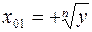

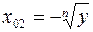Однако, если область определения P функции y = xⁿ разбить на два подмножества P ₁ = [0, +∞) и P ₂ = (– ∞, 0) и область определения функции y = xⁿ ограничить этими подмножествами, то на каждом из этих подмножеств функция y = xⁿ имеет обратную функцию.

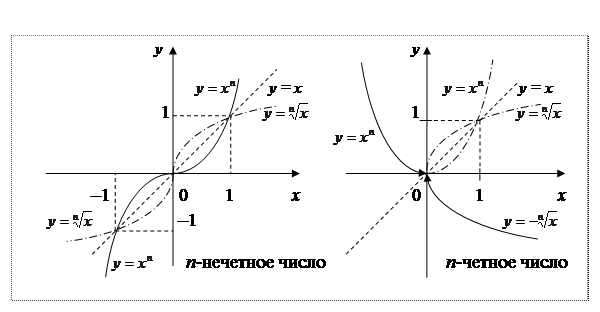
Рис. 3 Рис. 4

На промежутке P ₁ обратной функцией является 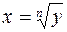, а на P ₂ – 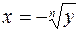. Графики прямой и обратной функций для области определения P ₂ показаны на рис.4 сплошной кривой, а для P ₁ – пунктирной. Следует обратить внимание на то, что область определения P ₂ представляет собой открытый интервал, так как для y ₀ = 0 соответствуют не два значения x из P, как для всех остальных y из E, а только одно: x = 0. Мы же точку ноль отнесли к первому промежутку. На графике на этот факт указывают стрелки при приближении к точке нуль.

3. y = sin x – тригонометрическая функция. График этой функции показан на рис.5. Как видно из графика, эта функция определена в промежутке P = (-∞,+∞), причем ее значения заполняют сплошь промежуток E =[-1,1]. Каждому значению y = y ₀из E отвечает бесконечное множество значений x из P. Поэтому функция y = sin x, определенная на P, обратной функции не имеет. Однако, если промежуток P разбить на бесконечное число промежутков 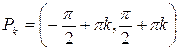, где k = 0, ±1, ±2,... (k Î Z), то функция y = sin x, определенная на каждом таком промежутке P_k, имеет обратную функцию, определенную на промежутке (–1,1) и со значениями в данном промежутке P_k. Что же касается граничных точек 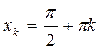, разделяющих промежутки P_k и P_{k+ 1}, то эти точки будем относить к промежутку P_k; тогда промежуток P_k будет замкнутым справа, а промежуток P_{k+ 1} открытым слева, если k = 0, 1, 2... и, соответственно, замкнутым слева, а открытым справа если k = –1, –2.... Обычно обратную функцию для y = sin x рассматривают лишь для промежутка k = 0, т.е. 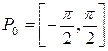. Обратим внимание, что это единственный замкнутый промежуток из всех разбиений P_k области Р. Каждому у ₀ из [–1,1] в пределах 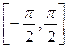отвечает одно значение х ₀₀; его обозначают через х ₀₀ = arcsin y ₀, а все множество значений х _{0 к} из Р, которым в соответствие ставится у ₀ из Е = [–1,1] записывают в виде х _{0 k} = (–1) ^k arcsin y ₀ + p k, k Î Z.

Таким образом, обратная функция для y = sin x, определенная на замкнутом промежутке [–1,1], со значениями в замкнутом промежутке 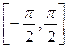имеет вид х = arcsin y (либо у = arcsin х). График функции у = arcsin х показан на рис.6.

Подобные рассуждения для остальных тригонометрических функций приводят к следующим результатам:

а) функция y = cos x, определенная на замкнутом промежутке Р ₀ = [0, p ], имеет обратную х = arccos у (либо у = arccos х), определенную на сегменте [1,1]. Множество всех значений х = х _{0 k} из Р = (-∞, +∞) соответствующих у = у ₀ из Е = [–1,1] записывается

х _{0 k} = ± arccos y ₀ + 2 p k, где k Î Z;

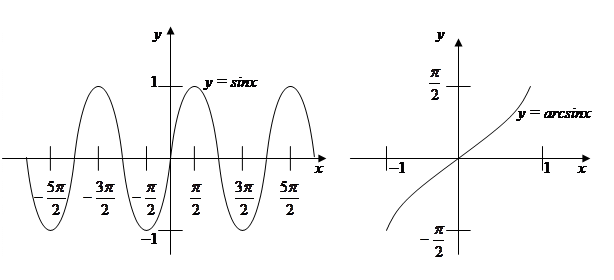
Рис. 5 Рис. 6

б) функция y = tg x, определенная на интервале 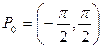имеет обратную x = arctg y (либо у = arcctg x), определенную на Е = (-∞, +∞). Множество значений х _{0 k} из Р соответствующих у ₀ из Е записывают

х _{0 k} = arcсtg y ₀ + pk, k Î Z.

Для значений 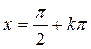функция у = tg x не определена;

в) функция у = ctg x; Р ₀ = (0, p), имеет обратную х = arcctg у (у = arcctgx), Е = (-∞, +∞). Для значений х = kp, k Î Z функция у = ctg x не определена, х _{0 k} = arcсtg y ₀ + kp.

Графики этих функций показаны на рис. 7 – 9.

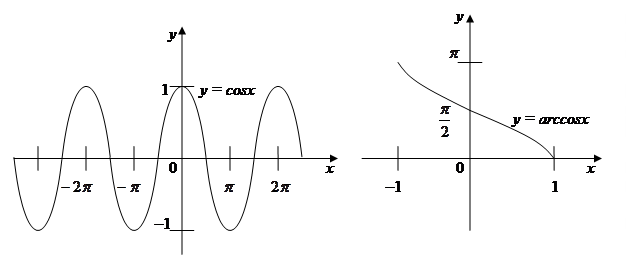
Рис. 7

Рис. 8 (Переделать, асимптоты)

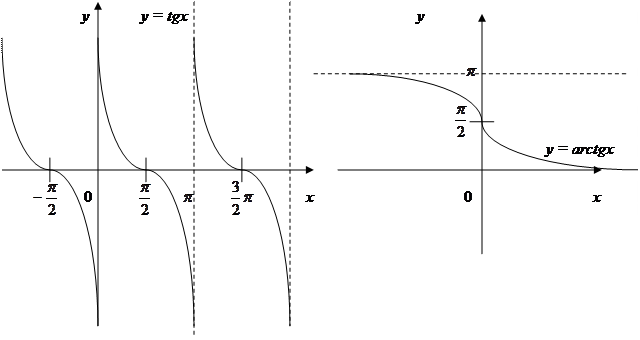
Рис. 9 (Переделать, асимптоты)

---

Дата добавления: 2015-07-20