Параметрическое задание функции

Пусть даны три числовых множества R Ì R, E Ì R, T Ì R с элементами х Î R, у Î Е, t Î T и две функции j и y такие, что х = j (t), у = y (t).

Пусть, кроме того, отображение j взаимно однозначно, т.е. для функции х = j (t) существует обратная функция t = j ^{– 1}(х). Тогда легко видеть, что и у оказывается функцией от х: y = y (j ^{– 1}(х)) = f (x).

В этом случае говорят, что функция у = f (x) задана параметрически; переменная t называется параметром, а выражения х = j (t) и у = y (t) – параметрическими уравнениями.

При параметрическом задании функции f можно, не восстанавливая непосредственной зависимости у от х так, как это было сделано выше, получить уравнение F (x, y) = 0, которое будет определять функцию у = f (x) неявно. Для этого необходимо из выражений х = j (t) и у = y (t) исключить параметр t. Например, пусть функция у = f (x) задана параметрическими уравнениями и , где ch t и sh t – гиперболические функции, соответственно косинус и синус (см. гл.1 §4, п.4.2). Определим отсюда ch t и sh t затем возведем обе части этих уравнений в квадрат и вычтем:

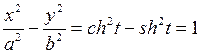(см. гл.1, §4, п.4.2).

Полученное уравнение 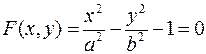и есть то уравнение, которое неявно задает функцию у = f (x).Это, как известно, уравнение гиперболы. Отсюда и происходит название «гиперболические функции».

Дата добавления: 2015-07-20