Читайте также:
|
Если члены последовательности суть значений монотонной числовой функции переменного п, то последовательность называется монотонной или, по типу монотонной функции соответственно: возрастающей, неубывающей, убывающей, невозрастающей последовательностями.
Для монотонной последовательности справедлива следующая теорема, условие которой является достаточным условием для сходимости (существования конечного предела) последовательности.
Теорема. Ограниченная монотонная последовательность всегда имеет конечный предел, т.е. является сходящейся.
Эту теорему примем без доказательства.
Если последовательность не является монотонной, то условие данной теоремы, как следует из теоремы 2 (п.5.2), является, лишь необходимым, но не достаточным.
Пример. Доказать, что последовательность 
имеет конечный предел, т.е. сходится.
Доказательство. Покажем, что эта последовательность ограничена. Представим ее общий член в виде
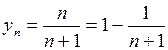, откуда 
или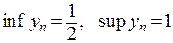 
.
Исследуем эту же последовательность на монотонность. Найдем разность
.
Таким образом,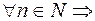 
yn+ 1 > yn, т.е. последовательность монотонно возрастающая. Тогда, по теореме, она имеет конечный предел или сходится. Как было уже доказано (пример гл.1, §5, п.5.1), 
.
Дата добавления: 2015-07-20; просмотров: 130 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Неопределенные степенно-показательные выражения | | | Принцип сходимости последовательности |