Читайте также:
|
Зададимся теперь вопросом об общем признаке существования конечного предела любой последовательности, т.е. отысканием такого условия для сходимости последовательности, которое обладало бы свойством необходимости и достаточности.
Поставленную задачу решает теорема Больцано-Коши, которую часто называют также принципом сходимости.
Теорема (Больцано-Коши). Для того чтобы последовательность 
вообще имела конечный предел, необходимо и достаточно, чтобы для каждого 
существовал такой номер 
, чтобы неравенство 
выполнялось лишь только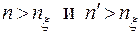 
.
Суть дела здесь в том, чтобы значения последовательности между собой безгранично сближались по мере возрастания их номера.
Доказательство теоремы опускаем.
Дата добавления: 2015-07-20; просмотров: 200 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Монотонные последовательности | | | УПРАЖНЕНИЯ |