УПРАЖНЕНИЯ. 1. Доказать, что множество ограничено.

1. Доказать, что множество ограничено.

2. Дана последовательность с общим членом .

а) Доказать, что ;

б) Будет ли эта последовательность монотонной?

в) Найдите sup y_n и inf y_n.

3. Дана последовательность с общим членом . Пользуясь вторым определением предела, доказать, что .

4. Доказать, что функции y = sin x и y = tg x периодические и определить их

периоды.

5. Найдите пределы:

а) ; б) ;

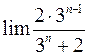в) ; г)

6. Доказать, что

7. Является ли последовательность бесконечно большой?

8. При каких условиях параметрические уравнения:

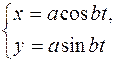а) ; б) ; в) ; г)

определяют функцию y = f (x)? Найти явный вид этих функций, а также уравнения F (x, y) = 0, посредством которых эти функции заданы неявно.

Дата добавления: 2015-07-20