Свойства функций, непрерывных на отрезке.

Приведем ряд основных свойств функций, непрерывных на отрезке (называемых глобальными, в отличие от локальных, рассматриваемых в п. 17.2).

Теорема 17.4. (О сохранении знака непрерывной функции).

Пусть функция y = f (x) непрерывна в точке х₀ и f (x₀) ¹ 0. Тогда существует такая d-окрестность точки х₀, что для всех
х Î функция f (x) имеет тот же знак, что и f (x₀) (см. рис. 17.9).

Доказательство. Пусть, для определенности, f (x₀) > 0. Т.к. f (x) непрерывна в точке х₀, т.е. , то

" e > 0 $ d > 0 " х: < d Þ < e, или f (x₀) - e < f (x) < f (x₀) + e.

Для e = получим: f (x) > f (x₀) - e = >0 для всех х Î . Аналогично доказывается для случая, когда f (x₀) < 0.

Теорема 17.5. (Первая теорема Больцано – Коши о нулях функции).

Пусть функция y = f (x) непрерывна на отрезке [ a,b ] и на концах отрезка принимает значения разных знаков: f (a) f (b) < 0. Тогда существует точка с Î (a,b) такая, что f (с) = 0.

Доказательство теоремы опустим. Приведем простой геометрический смысл этой теоремы: непрерывная кривая (график непрерывной функции) при переходе с одной полуплоскости в другую обязательно пересечет ось Ох (см. рис. 17.10).

Теорема 17.6. (Вторая теорема Больцано – Коши о промежуточном значении).

Пусть функция y = f (x) непрерывна на отрезке [ a,b ], причем f (a) =А, f (b) = В. Пусть с –любое число, заключенное между А и В. Тогда существует точка с Î [ a,b ] такая, что f (с) = с.

Доказательство. Пусть для определенности А < В и А < C < В (см. рис. 17.11).Тогда функция y = j (x) = f (x) - C непрерывна на отрезке [ a,b ] и на его концах принимает значения разных знаков: j (а) = f (а) – C = А – C < 0, j (b) = f (b) – C = = B – C > 0. По теореме 17.5 существует точка с Î (a,b) такая, что j (с) = f (с) - C = 0, т.е. f (с)= C.
Другими словами, непрерывная функция при переходе от одного знака к другому принимает и все промежуточные значения (графически это означает, что прямая y = C обязательно пересечет график непрерывной функции, как это изображено на рис. 17.11).

Напомним, что непрерывная в точке х₀ функция y = f (x), ограничена в некоторой окрестности этой точки (ограниченность функции, имеющей предел, теорема 16.1). Для функций, непрерывных на отрезке, справедлива следующая теорема.

Теорема 17.7.(Первая теорема Вейерштрасса).

Если функция y = f (x) непрерывна на отрезке [ a,b ], то она ограничена на этом отрезке, т.е. существуют числа т и М такие, что т < f (x) < М для всех x Î [ a,b ].

Примем теорему без доказательства.

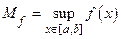Если точная верхняя и точная нижняя границы множества значений функции сами являются значениями функции, то мы говорим, что функция достигает своих точных границ. Пусть, как и прежде, и – соответственно точная нижняя и точная верхняя границы.

Теорема 17.8. (Вторая теорема Вейерштрасса о достижении наибольшего и наименьшего значений).

Если функция y = f (x) непрерывна на отрезке [ a,b ], то она достигает на этом отрезке своих точных верхней и нижней границ, которые являются соответственно наибольшим и наименьшим значениями функции на отрезке [ a,b ], т.е. $ х₁, х₂ Î [ a,b ] такие, что

f (x₁) = 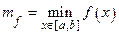, f (x₂) = .

Доказательство. Согласно теореме 17.7 функция y = f (x) будет непрерывна, ограничена на отрезке [ a,b ], поэтому существуют точные верхняя и нижняя границы множества значений функции (см. теорему 13.1). Обозначим их, как и раньше, 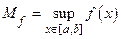и соответственно. Ясно, что для каждого значения аргумента x Î [ a,b ] выполняется неравенство: т_f £ f (x) £ М_f.

Покажем, что функция y = f (x) достигает М_f, т. е. существует точка x₀ Î [ a,b ] такая, что
f (x₀) = М_f. Доказательство проведем "от противного". Пусть ни в одной точке отрезка [ a,b ] функция y = f (x) не принимает значения, равного М_f. Тогда f (x) < М " x Î [ a,b ].

Рассмотрим на отрезке [ a,b ] непрерывную и положительную функцию . По теореме 17.7 функция y = F (x) ограничена на отрезке [ a,b ], т. е.
$m > 0: F (x) £ m " x Î [ a,b ], или £ m, отсюда следует, что f (x) £ М_f - .

Это означает, что число М_f - является верхней границей множества значений функции y=f (x). Но это противоречит тому, что М_f – точная верхняя граница этого множества, т. е. наименьший элемент во множестве всех верхних границ. Полученное противоречие доказывает, что на отрезке [ a,b ] существует точка x₀ Î [ a,b ] такая, что f (x₀) = М_f.

Аналогично доказывается, что $ x₁ Î [ a,b ]: f (x₁) = т_f. Доказательство полностью закончено.

Следствие 17.1. Непрерывная функция y = f (x) отображает отрезок [ a,b ] на отрезок
[ т_f;М_f ], где т_f и М_f соответственно точная нижняя и точная верхняя границы множества значений функции.

Это сразу вытекает из вышеприведенной теоремы 17.8 и теоремы 17.6 о промежуточном значении.

Дата добавления: 2015-07-20