Непрерывность основных элементарных функций.

1. Постоянная функция у=f (x) =С, где С = const непрерывна на множестве R = , т. к. в каждой точке х₀Î R (cм. пример 16.1), что и означает непрерывность функции в точке х₀.

2. Функция у=f (x) = х непрерывна на R, т.к. " х₀Î R $ (см. пример 16.2).

3. Функция у=f (x) = х^k, k Î N непрерывна на R, т.к." х₀Î R $ (см. пример 16.6).

4. Многочлен степени п P_n (x) = 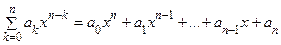является

непрерывной функцией на R, т.к. $ (см. пример 16.7).

5. Дробно-рациональная функция (рациональная дробь) является непрерывной функцией в каждой точке, в которой знаменатель не обращается в ноль. Это следует из теоремы 17.1 и того факта, что числитель Q_m (x) рациональной дроби, являясь многочленами, непрерывны всюду на R.

6. Функция у = f (x) = sin x непрерывна на множестве R. Действительно, если х₀ – произвольная фиксированная точка, то Dу = sin (x₀ + Dx) – sin x₀ = , где ~ , а функция у = является ограниченной на R. Тогда

как произведение б. м. функции на ограниченную функцию (см. осовные свойства б. м. функций, п. 16.4). Но это и означает непрерывность функции у = sin x в каждой точке числовой оси.

7. Функция у = f (x) = cos x непрерывна на множестве R, т. к. ее можно представить в виде у = cos x = sin и воспользоваться теоремой 17.2 о непрерывности сложной функции; где у = sin x и непрерывны.

8. Функция у = tg x непрерывна всюду на R, кроме точек , п ÎZ. Это следствие того, что tg x = есть отношение двух непрерывных функций, и теоремы 17.1.

9. Функция у = f (x) = arcsin x непрерывна на отрезке [-1;1] по теореме 17.3 о непрерывности обратной функции. Действительно, функция у = sin x монотонно возрастает и непрерывна на отрезке , а множество ее значений есть отрезок [-1;1] (см. рис. 17.2). Поэтому обратная функция у = arcsin x возрастает и непрерывна на отрезке [-1;1].

Аналогично можно показать, что функции у =
= arccos x и у = arctg x непрерывны в области своего определения как обратные к у = cos x и у = tg x соответственно.

10. Функция y = a^x, a >0 и a ¹ 1, непрерывна и монотонна на R: возрастает при a >1 и убывает при
0 < a < 1. Поэтому обратная функция y = log_a x монотонна и непрерывна при х > 0.

11. Степенная функция у = f (x) = х^a , a ÎR, непрерывна на множестве (0;+¥) по теореме о непрерывности сложной функции, т. к. , а функции у = f (t) =a^t и

и t = j (x) = a log_a x непрерывны.

Итак, мы доказали непрерывность основных элементарных функций.

Напомним, что элементарной мы назвали функцию, образованную из основных элементарных функций и действительных чисел с помощью конечного числа арифметических действий и образования сложной функции. Поэтому из всего вышесказанного вытекает следующий важный вывод: всякая элементарная функция непрерывна в каждой точке, в которой она определена.

Отсюда следует, что при нахождении предела элементарной функции в точке, в которой она определена, нужно просто вычислить значение элементарной функции в этой точке.

Дата добавления: 2015-07-20