Односторонние пределы.

Мы дадим определение предела функции в точке в случае, когда функция определена в (двусторонней) окрестности этой точки:

а аргумент х стремится к х ₀ любым способом, в частности, колеблясь около точки х ₀.

Дадим определение предела функции в точке в случае, когда функция определена в левой окрестности точки (предел слева) или в правой окрестности (предел справа) рассматриваемой точки:

Число А называется пределом функции y=f (x) в точке х ₀ слева, если для любого e>0 существует d>0 такое, что для любого х ₀Î(х ₀-d, х ₀), выполняется неравенство | f (x)- A |<e (см. рис. 16.5.).

Предел слева обозначается f (x ₀-0) и пишут:

f (x ₀-0)= 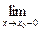f (x)= А,

где x → x ₀-0 означает, что х→х ₀ и x < x ₀.

Число А называется пределом функции f (x) в точке х ₀ справа, если для любого числа e>0 существует d>0 такое, что для любого х ₀Î(х ₀, х ₀+d), выполняется неравенство | f (x)- A |<e (см. рис. 16.5.).

Предел слева обозначается f (x ₀+0) и пишут:

f (x ₀+0)= f (x)= А,

где x → x ₀+0 означает, что х→х ₀ и x > x ₀.

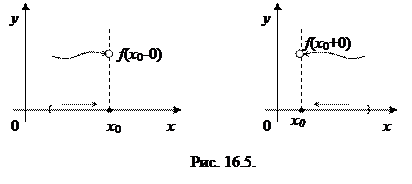
Пределы функции слева и справа называются односторонними пределами.

Теорема 16.6. $ f (x)= А ó $ f (x ₀+0), f (x ₀-0) и f (x ₀-0)= А = f (x ₀+0). Другими словами, функция у=f (x) имеет предел в точке х ₀, равный А, тогда и только тогда, когда существуют односторонние пределы f (x ₀ ± 0) и они равны между собой (см. рис. 16.6.).

Если х ₀=0, то вместо 0-0 пишем -0, а вместо 0+0 пишем +0.

Пример 16.12. Рассмотрим функцию у = f (x)=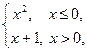

Найдем пределы слева и справа в точке х ₀ = 0:

f (-0)= 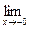f (x)= 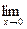х ² = 0 = f (0),

f (+0)= f (x) = 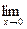(х +1) = 1 и f (-0) ≠ f (+0),

т.е. в точке х ₀ =0 функция предела не имеет (см. рис. 16.17.).

Дата добавления: 2015-07-20