Некоторые важнейшие функциональные зависимости.

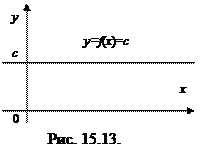15.5.1. Постоянная функция. Функция у=f (x)= c, принимающая для всех значений аргумента х одно и тоже постоянное значение с, называется постоянной функцией, а ее графиком служит прямая называется постоянной функцией, а ее графиком служит прямая у = с, параллельная оси Ох (см. рис. 15.13).

15.5.2. Линейная функция и прямая пропорциональная зависимость.

Прямой пропорциональной зависимостью называется функция, задаваемая формулой у=кх, где к ≠0. графиком этой зависимости служит прямая линия, проходящая через начало координат (см. рис. 15.14). Величина у пропорциональна величине х, т.е. если у ₁ = кх ₁, а у ₂ = кх ₂, то

,

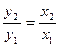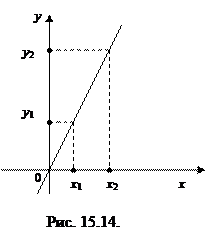а построенный коэффициент к называется коэффициентом пропорциональности. Если у = кх, то х= 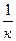у, т.е. х пропорционально у, но с обратным коэффициентом пропорциональности.

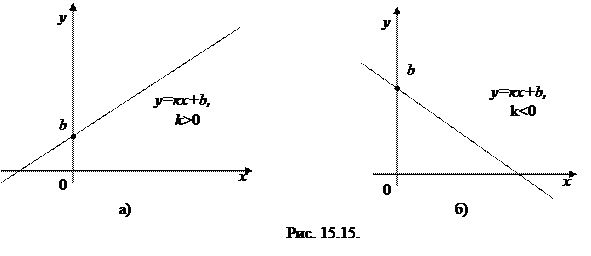
Линейной функцией называется функция у = кх+b, где k,b – постоянные, х Î R. Как мы знаем из аналитической геометрии, графиком ее служит прямая линия, к – угловой коэффициент этой прямой, b – отрезок, отсекаемый на оси Оу. При к >0 линейная функция возрастает, а при k <0 – убывает (см. рис. 15.15):

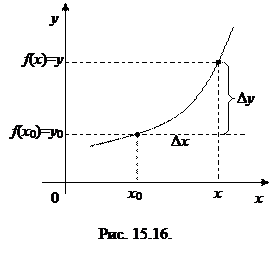Прежде чем сформулировать одно важное свойство линейной функции, напомним понятия приращения аргумента и соответствующего ему приращения функции. Пусть задана функция y=f (x), х Î(a, b). Выберем и зафиксируем некоторое значение аргумента х ₀Î(a, b), а y ₀ = f (x ₀)– соответствующее значение функции. Выберем другое значение аргумента х, а y=f (x) – соответствующее значение функции (см. рис. 15.16). Число

D х=х-х ₀

называется приращение аргумента, а число

D у=f (x)- f (x ₀)= f (x ₀+D х)- f (x ₀)

называется приращением функции, соответствующим приращению аргумента D х. Обращаем внимание на тот факт, что приращение функции зависит от приращения аргумента (и точки х ₀, в которой это приращение вычисляется).

Теперь сформулируем то важное свойство линейной зависимости, о котором шла речь выше.

Приращение линейной функции пропорционально приращению аргумента и не зависит от начального значения аргумента.

Действительно, если D х=х-х ₀, х=х ₀+D х, то

D у=f (x)- f (x ₀)= f (x ₀+D х)- f (x ₀)= k (x ₀+D х)+ b - (kx ₀+ b)= k x ₀+ к D х+b - kx ₀- b = k D х,

т.е.

D у = к D х,

что и требовалось доказать.

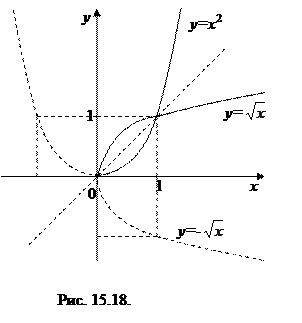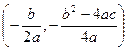15.5.3. Квадратичная функция. Квадратичной функцией называется функция вида y = ax ²+ bx+c, где a, b, c – постоянные и а ≠0. Графиком квадратичной функции является парабола с вершиной в точке М ₀ . Если а >0, то ветви параболы направлены вверх, при а <0 – вниз. На рис. 15.17. приведен график параболы у=х ². На промежутке (-¥, 0] эта функция убывает, а на промежутке [0, +¥)– возрастает. Не являясь взаимно однозначной, функция у=х ² не имеет обратной. Однако, если рассмотрим функцию у=х ² на промежутке [0, +¥), то она взаимно однозначна и имеет обратную: у= 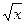, х Î[0, +¥).

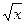График обратной функции у= симметричен графику функции у=х ² относительно биссектрисы первого и третьего координатных углов (см. рис. 15.18).

Тем самым, выделена однозначная ветвь функции.

у

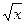Другая однозначная (и обратимая) ветвь получится, если рассмотреть нашу функцию у=х ² на промежутке (-¥, 0], тогда обратная функция имеет вид у= - (на рис 15.18.они изображены пунктиром).

15.5.4. Обратная пропорциональная зависимость. Обратной пропорциональной зависимостью называется функциональная зависимость, выражаемая формулой у= 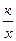, где к ≠0.

Если у ₁ = 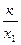и у ₂ = 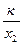, то 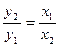, т.е. величина у обратно пропорциональна величине х, а число к называется коэффициентом обратной пропорциональности. Графиком этой функции служит гипербола. На рис. 15.19. изображен график функции у= 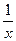. Оси координат Ох и Оу являются асимптотами гиперболы. Свойства асимптот гиперболы рассмотрены в пункте 9.3.

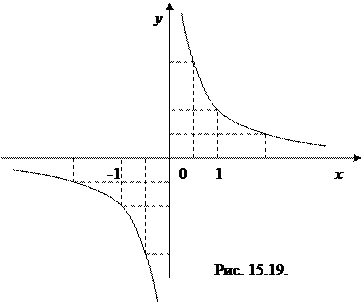
15.5.5. Показательная и логарифмическая функции.

Функция, заданная формулой у=а^х, где а >0, a ≠ 1, называется показательной функцией с основанием а.

Основные свойства показательной функции:

1) Область определения – множество R действительных чисел, множество значений – множество всех положительных чисел (0, +¥).

2)

При а >1 функция возрастает на всей числовой оси, при 0< a <1 функция убывает (см. рис. 15.20 а, б). График показательной функции проходят через точку (0;1) при всех а.

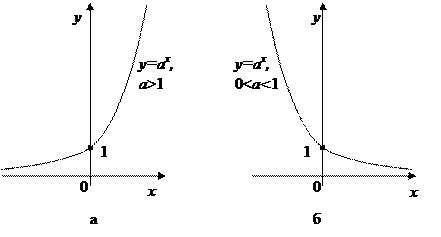3)

Ось Ох с уравнением у =0 является асимптотой графика показательной функции.

4) Для любых чисел х, у Î R справедливы равенства

а ^ха ^у=а ^х+у, 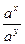= а ^х-у, (а ^х) ^у = а ^ху, а ⁰=1, а ^хb ^x =(аb) ^х, = ,
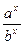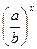a ^-1= = .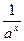

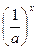Функция, заданная формулой y= log _a x, a >0, a ≠1, называется логарифмической функцией с основанием а.

Напомним, что логарифмом числа b по основанию а называется показатель степени с, в которую нужно возвести основание а, чтобы получить число b, т.е.

log _a b=c: a ^c= b или 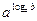= b.

Последняя формула называется основным логарифмическим тождеством. Из определения ясно, что определены логарифмы только положительных чисел b >0.

Основные свойства логарифмической функции:

1) Область определения – множество всех положительных чисел (0, +¥); множество значений – множество всех действительных чисел.

2) Логарифмическая функция на всей области определения возрастает при а >1 и убывает при 0< a <1 (см. рис. 15.21. а, б)

3) Ось Оу с уравнением х =0 является асимптотой графика показательной функции.

4) При любом а >0, а ≠1, и любых х >0 и y >0 выполняются равенства:

log _a 1=0, log _a а =1, log _a хⁿ = n log _a х, log _a (ху)= log _a х+ log _a у,

log _a 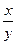= log _a х - log _a у, log _a b= 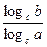(переход к другому основанию),
log _a b= .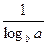

Из определения логарифмической функции вытекает, что

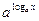= х, " х >0; 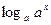= х, " х Î R,

и что функция у=а^х и у= log _a х являются взаимно обратными, а их графики симметричны относительно биссектрисы у=х первого и третьего координатных углов (см. рис. 15.22 а, б, соответствующие случаям а= 2 и а= )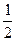

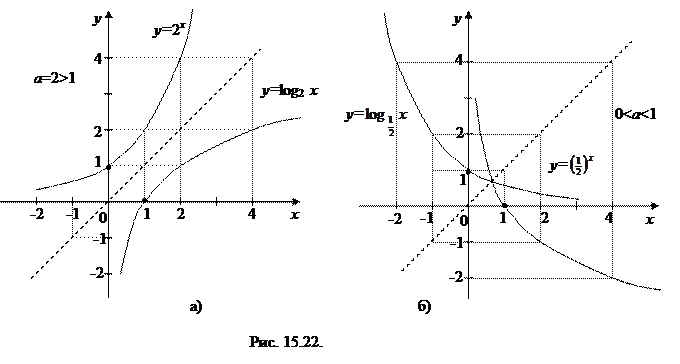
Дата добавления: 2015-07-20