Тригонометрические и обратные тригонометрические функции.

Напомним, что основные тригонометрические функции были определены в геометрии как отношения в прямоугольном треугольнике (см. рис. 15.23):

sin α = , cos α = , tg α = = ,
ctg α = = ,

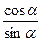Выполняется основное тригонометрическое тождество

sin² α + cos² α= 1.

15.5.6.1. Функция у= sin x и y= arcsin x.

Функция у= sin x определена на всей числовой оси, D (f) = R, E (f) = [-1, 1], т.е. у= sin x ограничена: -1≤sin x ≤1; нечетная: sin (- x) = -sin x; периодическая с периодом Т =2 p:
sin (x+ 2p n) = sin x " n Î Z.

Графиком функции у= sin x является синусоида, изображенная на рис. 15.24:

Как видно из графика, функция у= sin x не является взаимно однозначной, а значит не имеет обратной. Уравнение sin x = а имеет бесконечное множество решений при а Î[-1, 1], задаваемое формулой

х = (-1) ⁿ arcsin a+p n, n ÎZ.

Рассмотрим функцию у= sin x на отрезке , на котором она возрастает и принимает все значения из отрезка [-1, 1]: D (f)= , E (f)=[-1, 1]. Тогда существует обратная функция у=j(х), D (f)=[-1, 1], E (f)= называется арксинусом: у=j(х) = arcsin х

Арксинусом числа а Î[-1, 1] называется такое число (угол) α Î , синус которого равен а:

arcsin a = α ó sin α =а.

На рисунке 15.25. изображены графики прямой и обратной функций:

Рассмотрим у= sin x, D (f)= , E (f)=[-1, 1], которая монотонно убывает, и, следовательно, имеет обратную функцию у = j ₁(х), D (f) = [-1, 1], E (f) = , которая, как видно из рис. 15.26, имеет вид: у=j ₁(х)= p - arcsin x, которая получается из формулы (15.1) при n =1.

В заключении заметим, что

sin (arcsin a)= a, a Î[-1, 1],

arcsin (sin x)= x, x Î .

15.5.6.2. Функции y = cos x и y = arcсos x.

Функция y = cos x = sin определена на всей числовой оси, множество значений отрезок [-1, 1], т.е. ограничена: -1≤ cos x ≤1; четная: cos (- x)= cos x; периодическая с периодом Т =2 p: cos (x+ 2 pn)=cos x " n Î Z.

График изображен на рисунке 15.27:

Уравнение y = cos а при а Î[-1, 1] имеет бесконечное множество решений, задаваемое формулой

x = ± arccos a +2 pn, n Î Z.

На отрезке [0, p ] функция y = cos а убывает и принимает все значения из отрезка [-1, 1], а значит имеет обратную функцию, называемую арккосинусом, y=j (х) = arccos x, с областью определения
D (j) = [-1, 1] и множеством значений E (j) = [0, p ] (см. рис. 15.28).

Арккосинусом числа а называется такое число из отрезка [0, p ], косинус которого равен а:

arccos a=a ó cos a = a.

Справедливы равенства:

cos (arccos a)= a, a Î[-1, 1],

arccos (cos x)= x, x Î[0, p ].

15.5.6.3. Функция y = tg x и y = arctg x.

Функция y = tg x определена для всех чисел х, для которых cos x ¹0, т.е. все числа, кроме + pn, n Î Z. Множество значений E (f)= R. Нечетная: tg (- x) = -tg x. Периодическая с периодом Т = p: tg (x+ pn) = tg x " n Î Z. Вертикальные прямые х= + pn являются асимптотами графика функции y = tg x (см. рис. 15.29).

Уравнение tg x = а имеет бесконечное множество решений, задаваемых формулой

х = arctg a+ pn, n ÎZ.

В интервале функция монотонно возрастает и имеет обратную, определенную на R со значениями в интервале называемую арктангенсом: y = j (x) = arctg x.

Арктангенсом числа а Î R называется такое число из интервала , тангенс которого равен а:

arctg a=a ó tg a = a.

Графиком взаимообратных функций изображены на рисунке 15.30.

Справедливы формулы:

tg (arctg a) = a, a Î R,

arctg (tg x) = x, x Î .

Дата добавления: 2015-07-20