
Читайте также:
|
Напомним некоторые методы построения графиков функций с помощью преобразования графиков известных функций.
Пусть дан график функции y = f (x).
1. y = f (x)+ b. Параллельный перенос графика функции y = f (x) вдоль оси Оу на b вверх при b >0 и на | b | вниз при b <0.
Это равносильно сдвигу оси Ох в противоположную сторону (что гораздо выгоднее, если исходный график сложный).
2. y = f (x-а). Параллельный перенос графика функций y = f (x) вдоль оси Ох на а вправо при а> 0 и на | а | влево при а <0. Это равносильно сдвигу оси Оу в противоположную сторону.
3. y = кf (x). Растяжение графика функции y = f (x) вдоль оси Оу при к >1 и растяжение при 0< k <1.
4. y = f (кx). Сжатие графика функции y = f (x) вдоль оси Ох при к >1 и растяжение при 0< k <1 в 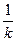 раз.
раз.
5. y = f (- x). Зеркальное отражение графика функции y = f (x) относительно оси Оу.
6. y = -f (x). Зеркальное отражение графика функции y = f (x) относительно оси Ох.
7. y = | f (x)|. Для получения этого графика из графика функции y = f (x), необходимо оставить без изменения участки графика y = f (x), лежащие выше оси Ох, а участки ниже оси Ох зеркально отразить относительно этой оси, т.к. | f (x)| = 
8. y = f (| x |). Строим сначала график функции y=f (x) при х ³0 и отражаем его зеркально относительно оси Оу.
Дата добавления: 2015-07-20; просмотров: 75 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тригонометрические и обратные тригонометрические функции. | | | Определение предела функции в точке. |