
Читайте также:
|
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  , за исключением, может быть, самой точки
, за исключением, может быть, самой точки  .
.
Определение 1: Предела функции (по Гейне) Число  называется пределом функции
называется пределом функции  в точке
в точке  (при
(при  ), если для любой последовательности
), если для любой последовательности  допустимых значений аргумента
допустимых значений аргумента  ,
,  , сходящийся к
, сходящийся к  ,
,  , соответствующая последовательность
, соответствующая последовательность 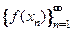 значений функции сходится к числу А:
значений функции сходится к числу А:  .
.
Обозначение: 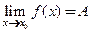 или
или  .
.
Определение 2 Предела функции (по Коши). Число  называется пределом функции
называется пределом функции  в точке
в точке  (при
(при  ), если для любого числа
), если для любого числа  существует число
существует число 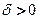 такое, что для всех допустимых значений аргумента
такое, что для всех допустимых значений аргумента  , удовлетворяющих неравенству
, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство 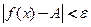 .
.
На языке кванторов это определение предела функции «на языке  » можно записать так:
» можно записать так:
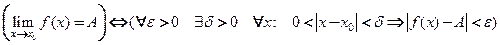 .
.
Заметив, что  выражает расстояние между числами
выражает расстояние между числами  и
и  , можно сказать, что
, можно сказать, что 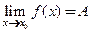 геометрически означает, что для всех
геометрически означает, что для всех  , достаточно близких к
, достаточно близких к  , соответствующие значения функции
, соответствующие значения функции 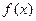 близки к числу А.
близки к числу А.
Определения 1 и 2 предела функции эквивалентны (примем без доказательства).
Рассмотрим примеры.
Пример 16.1. Постоянная функция  имеет предел в каждой точке
имеет предел в каждой точке  , равный С. Действительно, для любой последовательности
, равный С. Действительно, для любой последовательности  , сходящейся к числу
, сходящейся к числу  ,
,  , соответствующая последовательность
, соответствующая последовательность  значений функций является постоянной,
значений функций является постоянной, 
 , и сходится к числу С,
, и сходится к числу С,  , т.е.
, т.е.  . Последнее равенство показывает, что предел постоянной функции в точке
. Последнее равенство показывает, что предел постоянной функции в точке  равен значению функции в этой точке.
равен значению функции в этой точке.
Пример 16.2. Функция 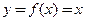 имеет в любой точке
имеет в любой точке  предел, равный
предел, равный  . Действительно, если последовательность
. Действительно, если последовательность  значений функций имеет вид
значений функций имеет вид  , что и доказывает утверждение. Заметим, что для функции
, что и доказывает утверждение. Заметим, что для функции 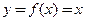 выполняется условие:
выполняется условие: 
 .
.
 Пример 16.3. Функция
Пример 16.3. Функция 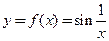 с областью определения
с областью определения 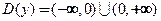 не имеет предела в точке
не имеет предела в точке 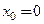 . Действительно, последовательность
. Действительно, последовательность 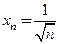 ,
,  , такова, что
, такова, что  и
и  , а последовательность
, а последовательность  ,
,  , такова, что
, такова, что  и
и  . Итак, мы построили две сходящиеся к нулю последовательности значений аргумента
. Итак, мы построили две сходящиеся к нулю последовательности значений аргумента  такие, что соответствующие последовательности значений функции имеют разные пределы. Но это означает, что функция
такие, что соответствующие последовательности значений функции имеют разные пределы. Но это означает, что функция 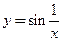 в точке
в точке 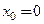 предела не имеет.
предела не имеет.
Пример 16.4. Функция  ,
, 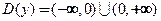 имеет в точке
имеет в точке 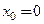 предел, равный нулю:
предел, равный нулю:  .
.
Действительно, покажем, что
 .
.
Так как 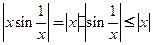 , то для
, то для 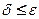 из неравенства
из неравенства  вытекает неравенство
вытекает неравенство
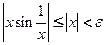 .
.
И это доказывает утверждение.
Введем понятие предела функции, когда аргумент стремиться к бесконечности:  ,
, 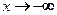 ,
,  .
.
Число А называется пределом функции  при
при  , если для любой бесконечно большой последовательности
, если для любой бесконечно большой последовательности  значений аргумента соответствующая последовательность
значений аргумента соответствующая последовательность  значений функции сходится к числу А.
значений функции сходится к числу А.
Обозначение: 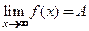
Итак,
 .
.
Аналогично определим предел при  :
:
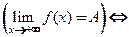
 ,
,

 .
.
Дата добавления: 2015-07-20; просмотров: 49 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Преобразование графиков функций. | | | Основные теоремы о пределах функций. |