
|
Читайте также: |
Варианты заданий
Задача 1
Найти область определения функции двух переменных
(дать геометрическое истолкование)
1.  . 2.
. 2. 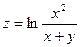 .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6. 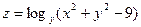 .
.
7. 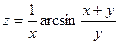 . 8.
. 8.  .
.
9. 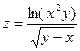 . 10.
. 10.  .
.
11.  . 12.
. 12.  .
.
13.  . 14.
. 14. 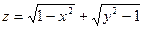 .
.
15.  . 16.
. 16.  .
.
17.  . 18.
. 18.  .
.
19. 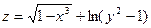 . 20.
. 20. 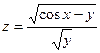 .
.
21.  . 22.
. 22.  .
.
23.  . 24.
. 24. 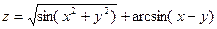 .
.
25.  . 26.
. 26. 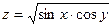 .
.
27.  . 28.
. 28.  .
.
29.  . 30.
. 30. 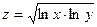 .
.
Задача 2
Найти частные производные  ,
, 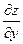 от функции
от функции  .
.
2.1.  . 2.2.
. 2.2. 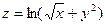 .
.
2.3. 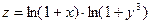 . 2.4.
. 2.4.  .
.
2.5.  . 2.6.
. 2.6.  .
.
2.7.  . 2.8.
. 2.8.  .
.
2.9.  . 2.10.
. 2.10.  .
.
2.11. 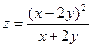 . 2.12.
. 2.12.  .
.
2.13.  . 2.14.
. 2.14.  .
.
2.15.  . 2.16.
. 2.16.  .
.
2.17.  . 2.18.
. 2.18. 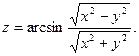
2.19.  . 2.20.
. 2.20.  .
.
2.21.  . 2.22.
. 2.22.  .
.
2.23. 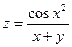 . 2.24.
. 2.24. 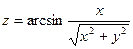 .
.
2.25.  . 2.26.
. 2.26. 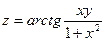 .
.
2.27. 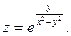 2.28.
2.28.  .
.
2.29. 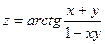 . 2.30.
. 2.30.  .
.
Задача 3. Вычислить производные сложных функций.
1.  где
где 



2.  где
где 


3.  , где
, где  ,
, 

4.  , где
, где 
 ;
; 
5.  где
где 
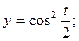

6.  где
где 
 ;
; 
7.  где
где 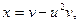
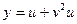 ;
; 

8.  где
где  ,
, 

9.  где
где  ,
,  ;
; 
10.  где
где 
 ;
; 
11. 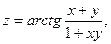 где
где 
 ;
; 
12.  где
где  ,
, 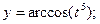

13. 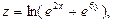 где
где 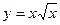 ;
; 

14.  где
где  ,
, 

15.  где
где 
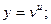


16.  где
где 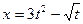 ,
, 

17.  где
где 
 ;
; 
18.  где
где 
 ;
; 
19.  , где
, где  ,
, 

20.  где
где 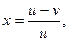



21.  где
где 


22.  где
где 
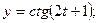

23.  , где
, где 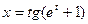 ,
, 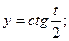

24. 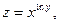 где
где 



25.  где
где  ,
, 

26.  где
где 
 ;
; 
27.  где
где 


28.  , где
, где 
 ;
; 
29.  , где
, где  ,
,  ;
; 
30. 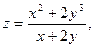 где
где 



Дата добавления: 2015-07-20; просмотров: 74 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Учитель ИЯ как субъект образовательного процесса. Педагогическое мастерство. | | | Задача 6. Экстремум, наибольшее и наименьшее значение. |