
Читайте также:
|
Очень часто в практической работе возникает необходимость найти в явном виде функциональную зависимость (формулу)  между величинами
между величинами  и
и  , которые заданы отдельными парами значений
, которые заданы отдельными парами значений  ,
,  (таблицей), например, полученными в результате измерений.
(таблицей), например, полученными в результате измерений.
Задача восстановления аналитической функции по отдельным значениям называется аппроксимацией. Для получения единственного решения задачи аппроксимации необходимо
1. Задать общий вид аппроксимирующей функции, включающий неизвестные параметры (коэффициенты). Вид функции задается, исходя из формы распределения аппроксимируемых значений (расположения точек на графике), из предполагаемой функциональной зависимости, или просто в виде полинома некоторой степени;
2. Определить значения параметров на основе заданного критерия близости. Здесь существует два основных подхода – интерполяция и сглаживание.
4.1. Интерполяция.

|
| Рис. 4.1. График интерполирующей функции проходит через заданные точки. |
Для задачи интерполяции критерий близости аппроксимирующей функции  к исходным данным
к исходным данным  ,
,  рассматривается как совпадение значений в заданных точках, называемых узлами интерполяции (рис. 4.1), т.е.
рассматривается как совпадение значений в заданных точках, называемых узлами интерполяции (рис. 4.1), т.е.
 .
.
Если функция задана в виде полинома, то он называется интерполяционным полиномом и может быть записан, например, в форме Лагранжа или Ньютона.
4.1.1. Интерполяционный полином в форме Лагранжа.
Пусть на некотором промежутке 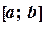 заданы
заданы  различных узлов
различных узлов  ,
, 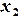 ,
,  , …,
, …,  , а также значения некоторой функции
, а также значения некоторой функции 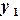 ,
, 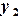 ,
,  , …,
, …,  в этих узлах. Необходимо построить полином
в этих узлах. Необходимо построить полином  , проходящий через заданные точки, т.е.
, проходящий через заданные точки, т.е.

Интерполяционный полином Лагранжа имеет следующую формулу:
 (4.1)
(4.1)
где 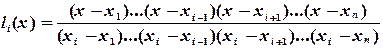 -фундаментальные полиномы Лагранжа. Они удовлетворяют равенствам
-фундаментальные полиномы Лагранжа. Они удовлетворяют равенствам
 (4.2)
(4.2)
и зависят лишь от заданных узлов  , но не от значений интерполируемой функции
, но не от значений интерполируемой функции  .
.
Пример 4.1. Пусть задана таблица:
| Таблица 4.1 | ||||

| 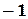
| 
| 
| |

| 
| 
| 
| 
|
Необходимо построить интерполяционный полином Лагранжа, проходящий через заданные точки
Решение. Полином Лагранжа имеет вид:

Найдем фундаментальные полиномы Лагранжа:
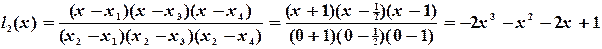

Подставляя 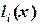 в полином Лагранжа, находим:
в полином Лагранжа, находим:

Дата добавления: 2015-07-25; просмотров: 74 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод Ньютона решения систем нелинейных уравнений. | | | Порядок решения. |