
Читайте также:
|
Что тут сказать… Если существует предел  , то функция
, то функция  называется бесконечно малой в точке
называется бесконечно малой в точке 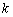 .
.
Существенным моментом утверждения является тот факт, что функция может быть бесконечно малойлишь в конкретной точке.
Начертим знакомую линию  :
:

Данная функция бесконечно малА в единственной точке: 
Следует отметить что, в точках «плюс бесконечность» и «минус бесконечность» эта же функция будет уже бесконечно большой: 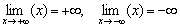 . Или в более компактной записи:
. Или в более компактной записи: 
Во всех других точках, предел функции будет равен конечному числу, отличному от нуля.
Таким образом, не существует такого понятия как «просто бесконечно малая функция» или «просто бесконечно большая функция». Функция может быть бесконечно малой или бесконечно большойтолько в конкретной точке.
! Примечание: для краткости я часто буду говорить «бесконечно малая функция», подразумевая, что она бесконечно малА в рассматриваемой точке.
Таких точек может быть несколько и даже бесконечно много. Изобразим какую-нибудь непуганую параболу:

Представленная квадратичная функция является бесконечно малой в двух точках – в «единице» и в «двойке»: 
Как и в предыдущем примере, на бесконечности данная функция является бесконечно большой: 
Смысл двойных знаков:
Запись  обозначает, что при
обозначает, что при  , а при
, а при  .
.
Запись  обозначает, что при
обозначает, что при 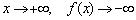 , а при
, а при  .
.
Запись  обозначает, что и при
обозначает, что и при  , и при
, и при  .
.
Запись 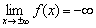 обозначает, что и при
обозначает, что и при  , и при
, и при  .
.
Прокомментированный принцип «расшифровки» двойных знаков справедлив не только для бесконечностей, но и для любых конечных точек, функций и ряда других математических объектов.
А теперь синус  . Это пример, когда функция бесконечно малА в бесконечном количестве точек:
. Это пример, когда функция бесконечно малА в бесконечном количестве точек:

Действительно, синусоида «прошивает» ось абсцисс через каждое «пи»:

Заметьте, что сверху/снизу функция ограничена, и не существует такой точки, в которой бы она была бесконечно большой, синусу остаётся разве что облизываться на бесконечность.
Отвечу ещё на пару простых вопросов:
Дата добавления: 2015-07-25; просмотров: 100 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод замены переменной в пределе | | | Может ли функция быть бесконечно малой на бесконечности? |