Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Может ли функция быть бесконечно малой на бесконечности?

Что необходимо знать и уметь на данный момент? | Что в пределах функций ЯВЛЯЕТСЯ неопределённостью и НЕ ЯВЛЯЕТСЯ неопределённостью | Порядок роста функции | Сравнение бесконечно больших функций | Сравниваем старшие степени: , следовательно, числитель более высокого порядка роста, чем знаменатель, и сразу можно сказать, что предел будет равен бесконечности. | Метод замены переменной в пределе | Что принципиально важно во всех рассмотренных примерах? | Замечательные эквивалентности в пределах | Первое правило Лопиталя | Второе правило Лопиталя |


Читайте также:
  1. A) не может быть произведена;
  2. A) обращать взыскание на любое имущество лица, на которое по закону может быть обращено взыскание;
  3. B. Как вы можете себя вести
  4. C) при сортовом помоле: после ситовеечного процесса может быть до 2% манной крупы от массы перерабатываемого зерна
  5. F52 Половая дисфункция, не обусловленная органическим расстройством или заболеванием
  6. I. Понятие малой группы. Виды и характеристика малых групп
  7. I. При каких условиях эта психологическая информация может стать психодиагностической?

Конечно. Таких экземпляров воз и маленькая тележка.
Элементарный пример: . Геометрический смысл данного предела, к слову, проиллюстрирован в статье Графики и свойства функций.

Может ли функция НЕ БЫТЬ бесконечно малой?
(в любой точке области определения )

Да. Очевидный пример – квадратичная функция, график которой (парабола) не пересекает ось 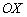. Обратное утверждение, кстати, в общем случае неверно – гипербола из предыдущего вопроса, хоть и не пересекает ось абсцисс, но бесконечно малА на бесконечности.

Дата добавления: 2015-07-25; просмотров: 57 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Бесконечно малые функции. Сравнение бесконечно малых| Сравнение бесконечно малых функций
mybiblioteka.su - 2015-2024 год. (0.006 сек.)