Что в пределах функций является неопределённостью и не является неопределённостью

Прежде всего, перед решением любого предела, обязательно выполняем подстановку «икса» в функцию – неопределённости может и не быть! Однако сладостей много вредно, и на первых двух уроках мы сталкивались со следующими неопределённостями:

Кроме указанных видов, существует довольно распространённая неопределённость («бесконечность минус бесконечность»), которую мы подробно разберём в этой статье, и совсем редко встречаются неопределённости .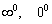

Для того чтобы устранить неопределённость, как вы знаете, необходимо использовать некоторые правила и методы решения пределов.

Теперь о том, ЧТО НЕ ЯВЛЯЕТСЯ неопределённостью.

Неопределённостью не является:

– Любая определённость =)

– Бесконечно малое число, делённое на ненулевую константу: 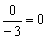. Сюда же можно отнести бесконечно малое число, делённое на бесконечно большое число:

– Ненулевая константа, делённая на бесконечно малое число, например: .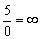

– Начинающие изучать математический анализ, часто пытаются устранить мифическую неопределённость . Но все попытки тщетны, поскольку это определённость:
представим «бесконечность делить на ноль» в виде произведения: , и, согласно предыдущему пункту: . Приведу живой пример:

Примечание: знак можно записать и без «плюса»: 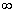. Это равноценные обозначения, и на практике используют оба варианта. Для более чёткого изложения в ряде примеров я буду ставить знак «плюс».

– Число, не равное единице, в бесконечно большой степени не является неопределённостью. Например: . В частности: .

– Разность двух функций, каждая из которых стремится к нулю, например: . Таким образом, неопределённости «ноль минус ноль» тоже не существует – это определённость.

Многие из перечисленных неопределённостей и определённостей уже встречались и ещё неоднократно встретятся на практике.

До нового 2013-го года остаются считанные дни, и в качестве подарка я принёс увесистый ящик с петардами:

Дата добавления: 2015-07-25