Сравнение бесконечно малых функций

В статье Методы решения пределов были подробно рассмотрены гиганты, которые мерялись между собой порядком роста, и ситуацию контролировала самая большая особь. Общество карликов устроено точно так же, только соревнуются они в другой весовой категории – порядке малости. Среди лилипутов тоже существуют свои великаны, кто самый крупный – тот и девушку танцует. Проясним ситуацию. Рассмотрим следующую бесконечно малую функцию:

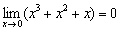
Да, совершенно понятно, что предел равен нулю, но обратим внимание на довольно любопытную вещь: в пределе находится сумма функций 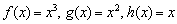, и некоторые из них будут стремиться к нулю быстрее, а некоторые – медленнее. Об этом я уже немного рассказывал в Примере №7 урока Методы решения пределов.

Построим последовательность 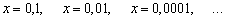, которая стремится к нулю, и вычислим несколько значений трёхчлена :

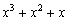Очевидно, что с уменьшением значений «икс», функция 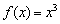убегает к нулю быстрее всех остальных (её значения обведены красным цветом). Говорят, что функция 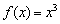более высокого порядка малости, чем функции 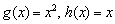, а также более высокого порядка малости, чем 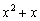. Но быстро бегать в Стране лилипутов – не есть доблесть, «тон задаёт» самый нерасторопный карлик 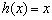, который, как и полагается боссу, идёт к нулю медленнее всех. Именно от него зависит, насколько быстро сумма 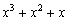приблизится к нулю:

Образно говоря, бесконечно малая функция 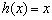«поглощает» всё остальное, что особенно хорошо видно по итоговому результату третьей строки. Иногда говорят, что 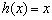более низкого порядка малости, чем 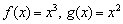и их сумма.

В рассмотренном пределе, всё это, конечно, не имеет особого значения, ведь в результате всё равно получается ноль. Однако «лилипуты-тяжеловесы» начинают играть принципиально важную роль в пределах с дробями. Начнём с примеров, которые, пусть редко, но встречаются в реальных практических работах:

Пример 1

Вычислить предел

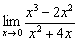
Здесь неопределённость 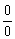, и из вводного урока о пределах функций вспоминаем общий принцип раскрытия данной неопределённости: нужно разложить числитель и знаменатель на множители, а потом что-нибудь сократить:

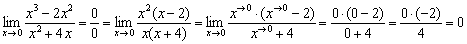
На первом шаге в числителе выносим за скобки 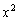, а в знаменателе «икс». На втором шаге сокращаем числитель и знаменатель на «икс», устраняя тем самым неопределённость. Указываем, что оставшиеся «иксы» стремятся к нулю, и получаем ответ.

В пределе получилась баранка, следовательно, функция числителя более высокого порядка малости, чем функция знаменателя. Или короче: числитель более высокого порядка малости, чем знаменатель. Что это значит? Числитель стремится к нулю быстрее, чем знаменатель, именно поэтому в итоге и получился ноль.

Как и в случае с бесконечно большими функциями, ответ можно узнать заранее. Приём аналогичен, но отличается тем, что в числителе и в знаменателе нужно МЫСЛЕННО отбросить все слагаемые со СТАРШИМИ степенями, поскольку, как отмечалось выше, определяющее значение имеют медленные карлики:

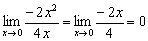
Пример 2

Вычислить предел

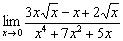
Ноль на ноль…. Давайте сразу узнаем ответ: МЫСЛЕННО отбросим все старшие слагаемые (быстрых карликов) числителя и знаменателя:

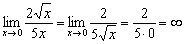
Алгоритм решения, точно такой же, как и в предыдущем примере:

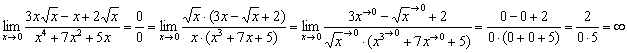
В данном примере знаменатель более высокого порядка малости, чем числитель. При уменьшении значений «икс», самый медленный карлик числителя (и всего предела) 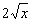становится настоящим монстром по отношению к своему более быстрому оппоненту 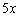. Например, если 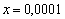, то 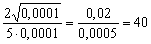– уже в 40 раз больше…. не монстр ещё, конечно, при данном значении «икс», но такой уже субъект с большим пивным животом.

И совсем простой демонстрационный предел:

Пример 3

Вычислить предел

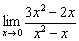
Узнаем ответ, МЫСЛЕННО отбросив все старшие слагаемые числителя и знаменателя:

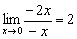
Решаем:

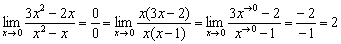
В результате получено конечное число. Хозяин числителя ровно в два раза толще начальника знаменателя. Это ситуация, когда числитель и знаменатель одного порядка малости.

На самом деле сравнение бесконечно малых функций давно фигурировало на предыдущих уроках:
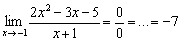(Пример №4 урока Пределы. Примеры решений );
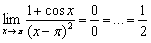(Пример №17 урока Методы решения пределов ) и т.д.

Напоминаю заодно, что «икс» может стремиться не только к нулю, но и к произвольному числу, а также к бесконечности.

Дата добавления: 2015-07-25