Читайте также:
|
Брат-2 борется с двумя спящими восьмёрками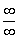 
. Аналогично:
Если существует предел отношения бесконечно больших в точке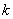 
функций: 
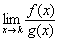, то в целях устранения неопределённости 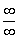можно взять две производные – ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. При этом: 
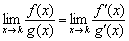, то есть при дифференцировании числителя и знаменателя значение предела не меняется.
Примечание: предел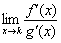 
должен существовать
Опять же, в различных практических примерах значение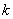 может быть разным, в том числе, бесконечным. Важно, чтобы была неопределённость .
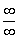Проверим Пример №3 первого урока: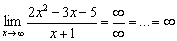 
. Используем второе правило Лопиталя:
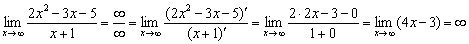
Однако для Примера №2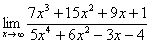 
той же статьи проверка данным способом будет весьма муторна. Тут придётся использовать правило Лопиталя три раза подряд (экспериментаторы могут попробовать). На самом деле ответ лежит на поверхности и почти мгновенно определяется устно (см. статью Методы решения пределов).
Коль скоро речь зашла о великанах, разберём два каноничных предела:
Пример 1
Вычислить предел
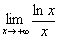
Получить ответ «обычными» методами непросто, поэтому для раскрытия неопределённости «бесконечность на бесконечность» используем правило Лопиталя:
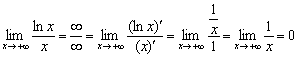
Таким образом, линейная функция более высокого порядка роста, чем логарифм с основанием бОльшим единицы (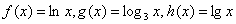
и т.д.). Разумеется, «иксы» в старших степенях тоже будут «перетягивать» такие логарифмы. Действительно, функция 
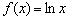растёт достаточно медленно и её график является более пологим относительно того же «икса».
Пример 2
Вычислить предел
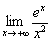
Ещё один примелькавшийся кадр. В целях устранения неопределённости 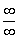, используем правило Лопиталя, причём, два раза подряд:
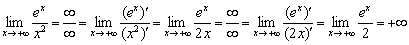
Дата добавления: 2015-07-25; просмотров: 78 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Первое правило Лопиталя | | | Показательная функция, с основанием, бОльшим единицы ( и т.д.) более высокого порядка роста, чем степенная функция с положительной степенью. |