Что принципиально важно во всех рассмотренных примерах?

Во-первых, предел должен вообще существовать в данной точке. Например, предела не существует. Если , то функция числителя 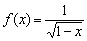не определена в точке «плюс бесконечность» (под корнем получается бесконечно большое отрицательное число). Подобные, казалось бы, вычурные примеры встречаются на практике: , как ни неожиданно, здесь тоже сравнение бесконечно малых функций и неопределённость «ноль на ноль». Действительно, если , то . …Решение? Избавляемся от четырёхэтажности дроби, получаем неопределённость и раскрываем её стандартным методом.

Возможно, начинающих изучать пределы сверлит вопрос: «Как так? Вот есть неопределённость 0:0, но на ноль же делить нельзя!». Совершенно верно, нельзя. Рассмотрим тот же предел 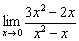. Функция 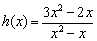не определена в точке «ноль». Но этого, вообще говоря, и не требуется, важно чтобы функция существовала В ЛЮБОЙ бесконечно близкой к нулю точке (или более строго – в любой бесконечно малой окрестности нуля). Само выражение «икс стремится к числу 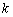» не всегда означает, что «икс» «строго» достигнет числа 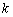, он может к нему бесконечно близко приближаться. Короче говоря – стремиться =)

Во-вторых, функции числителя и знаменателя должны быть бесконечно малЫ в данной точке. Так, например, предел совсем из другой команды, здесь функция числителя не стремится к нулю: .

Систематизируем информацию о сравнении бесконечно малых функций:

Пусть – бесконечно малые функции в точке 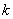(т.е. при ) и существует предел их отношений . Тогда:

1) Если , то функция более высокого порядка малости, чем .
Простейший пример: , то есть кубическая функция более высокого порядка малости, чем квадратичная.

2) Если , то функция более высокого порядка малости, чем .
Простейший пример: , то есть квадратичная функция более высокого порядка малости, чем линейная.

3) Если , где – ненулевая константа, то функции имеют одинаковый порядок малости.
Простейший пример: , иными словами, карлик бежит к нулю строго в два раза медленнее, чем , и «дистанция» между ними сохраняется постоянной.

Наиболее интересен частный случай, когда . Такие функции называют бесконечно малымиэквивалентнымифункциями.

Перед тем как привести элементарный пример, поговорим о самом термине. Эквивалентность. Данное слово уже встречалось на уроке Методы решения пределов, в других статьях и встретится ещё неоднократно. Что такое эквивалентность? Существует математическое определение эквивалентности, логическое, физическое и т.д., но попытаемся понять саму сущность.

Эквивалентность – это равнозначность (или равноценность) в каком-нибудь отношении. Самое время размять мышцы и немного отдохнуть от высшей математики. Сейчас на улице хороший январский морозец, поэтому очень важно хорошо утеплиться. Пожалуйста, пройдите в прихожую и откройте шкаф с одеждой. Представьте, что там висят два одинаковых тулупа, которые отличаются только цветом. Один оранжевый, другой фиолетовый. С точки зрения своих согревающих качеств, данные тулупы являются эквивалентными. И в первом, и во втором тулупе вам будет одинаково тепло, то есть выбор равноценен, что оранжевый надеть, что фиолетовый – без выигрыша: «один к одному равно одному». Но вот с точки зрения безопасности на дороге тулупы уже не эквивалентны – оранжевый цвет лучше заметен водителям транспорта, …да и патруль не остановит, потому что с обладателем такой одежды и так всё понятно. В этом отношении можно считать, что тулупы «одного порядка малости», условно говоря, «оранжевый тулуп» в два раза «безопаснее» «фиолетового тулупа» («который хуже, но тоже заметен в темноте»). А если выйти на мороз в одном пиджаке и носках, то разница будет уже колоссальной, таким образом, пиджак и тулуп – «разного порядка малости».

…зашибись, нужно запостить в Википедии со ссылкой на данный урок =) =) =)

Напрашивающийся пример бесконечно малых эквивалентных функций вам хорошо знаком – это функции первого замечательного предела .

Дадим геометрическое истолкование 1-го замечательного предела. Выполним чертёж:

Ну вот, крепкая мужская дружба графиков виднА даже невооруженным взглядом. А бесконечно близко вблизи нуля их и мама родная не отличит. Таким образом, если , то функции бесконечно малЫ и эквивалентны. А если разница ничтожно мала? Тогда в пределе синус вверху можно заменить «иксом»: , или «икс» внизу синусом: 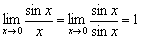. По сути, получилось геометрическое доказательство первого замечательного предела =)

Аналогично, кстати, можно проиллюстрировать любой замечательный предел, который равен единице.

! Внимание! Эквивалентность объектов не подразумевает совпадение объектов! Оранжевый и фиолетовый тулупы эквивалентно теплЫ, но это разные тулупы. Функции практически неотличИмы вблизи нуля, но это две разные функции.

Дата добавления: 2015-07-25